Three Fish Limit
Some friends are camping near the shore. One friend suggests that they go fishing. Six boats are available at the campsite. Each boat holds two people and the friends are excited because that is exactly how many they need. The rule on this lake is that each person can catch only three fish. How many fish did the friends catch that day if each friend caught the limit? Show all your mathematical thinking.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
A student may independently select a printed number line, number chart, ten frames, graph paper, etc. as they work on a task.
Suggested Materials
Engagement Image:
Teachers may project the images below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.
Possible Solutions
Assess
Novice
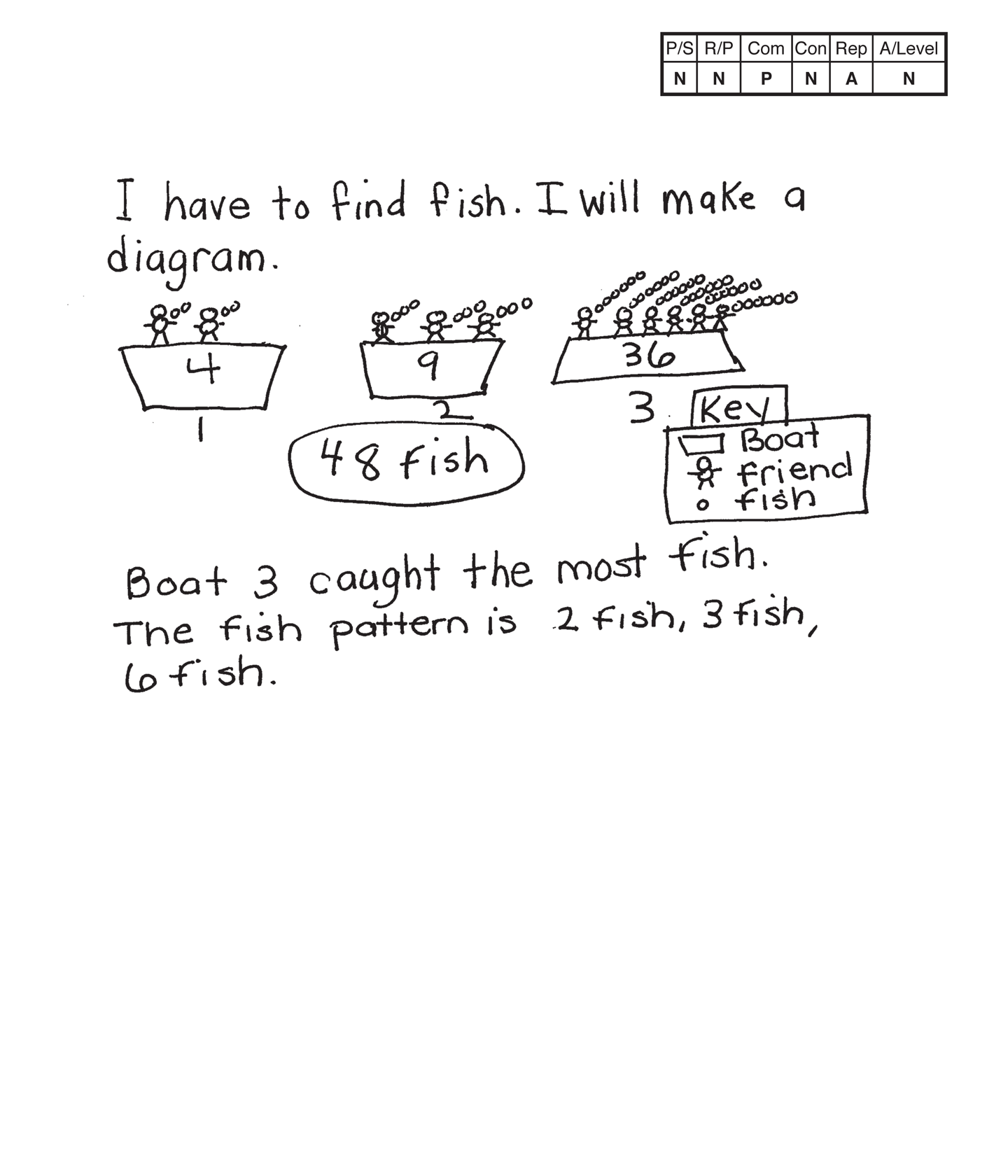
Novice 1
Scoring Rationale
Problem Solving
Novice
The student's strategy of using a diagram to show three boats with two friends in a boat catching two fish each, three friends in a boat catching three fish and six friends in a boat catching six fish would not work to solve this task. The student's answer, "48 fish," is not correct.
Reasoning & Proof
Novice
The student does not show any correct conceptual understanding of the problem. It appears that the student confuses three fish with three boats and then has the friends catch a number of fish equal to the number of friends in each boat.
Communication
Practitioner
The student correctly uses the mathematical terms diagram and key. Although the diagram represents incorrect data, the use of the communication terms is correct.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Apprentice
The use of a diagram is appropriate to this task but the student's work is not correct. The student does not represent six boats with two friends in each boat and each friend catching three fish.
Overall Achievement Level:
Novice
Apprentice
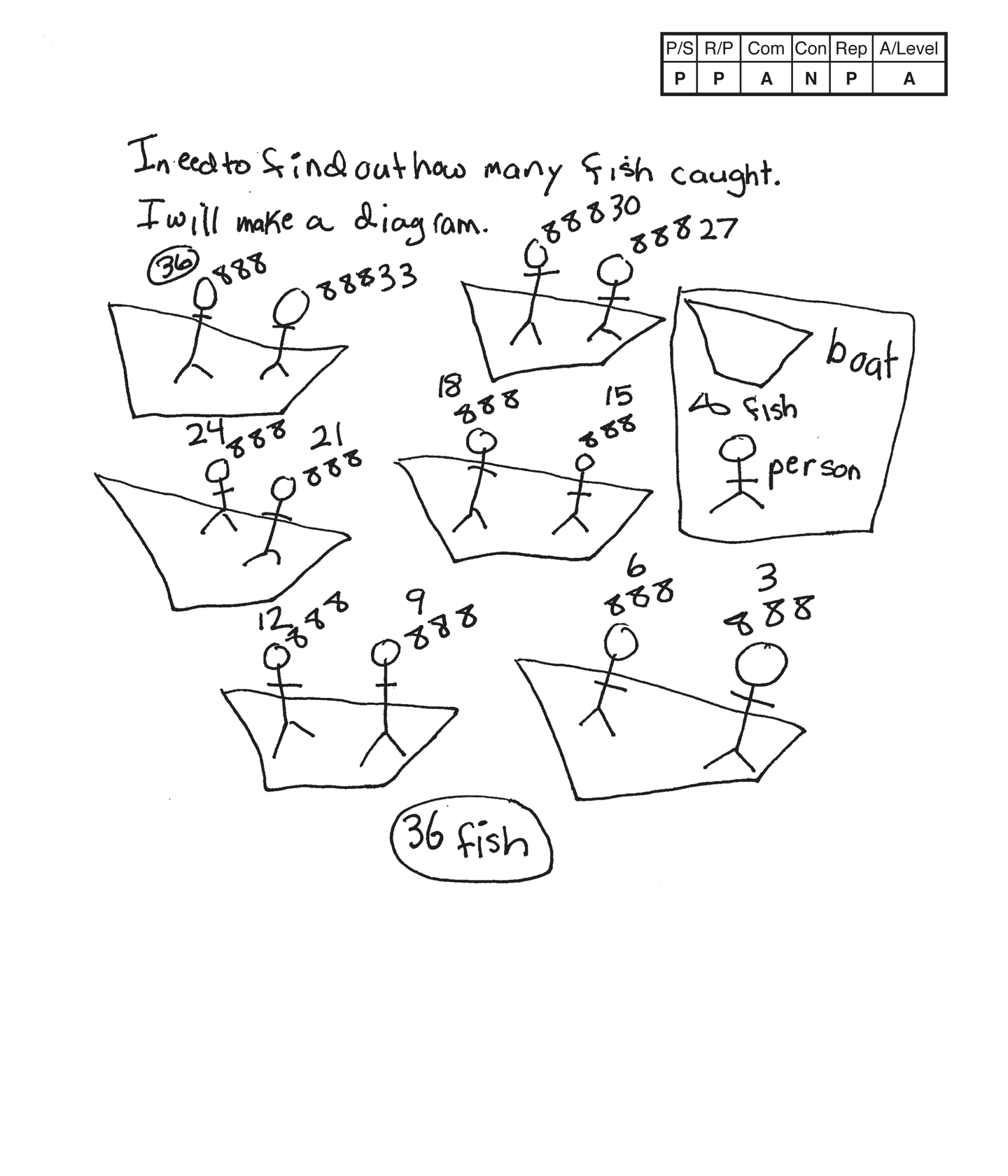
Apprentice 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a diagram and a key to represent the six boats, two friends per boat, and three fish per friend would work to solve this task. The student states a correct answer, "36 fish."
Reasoning & Proof
Practitioner
The student's arguments are constructed with adequate mathematical basis. The student’s solution is systematic and supports correct reasoning.
Communication
Apprentice
The student correctly uses the mathematical term diagram.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Practitioner
The student's diagram is appropriate and accurate. The student provides labels in a key for a boat, fish, and person. The student does not have to use the term key, but it would have provided another mathematical term to the student's solution.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for "Using the Assessment Rubric."
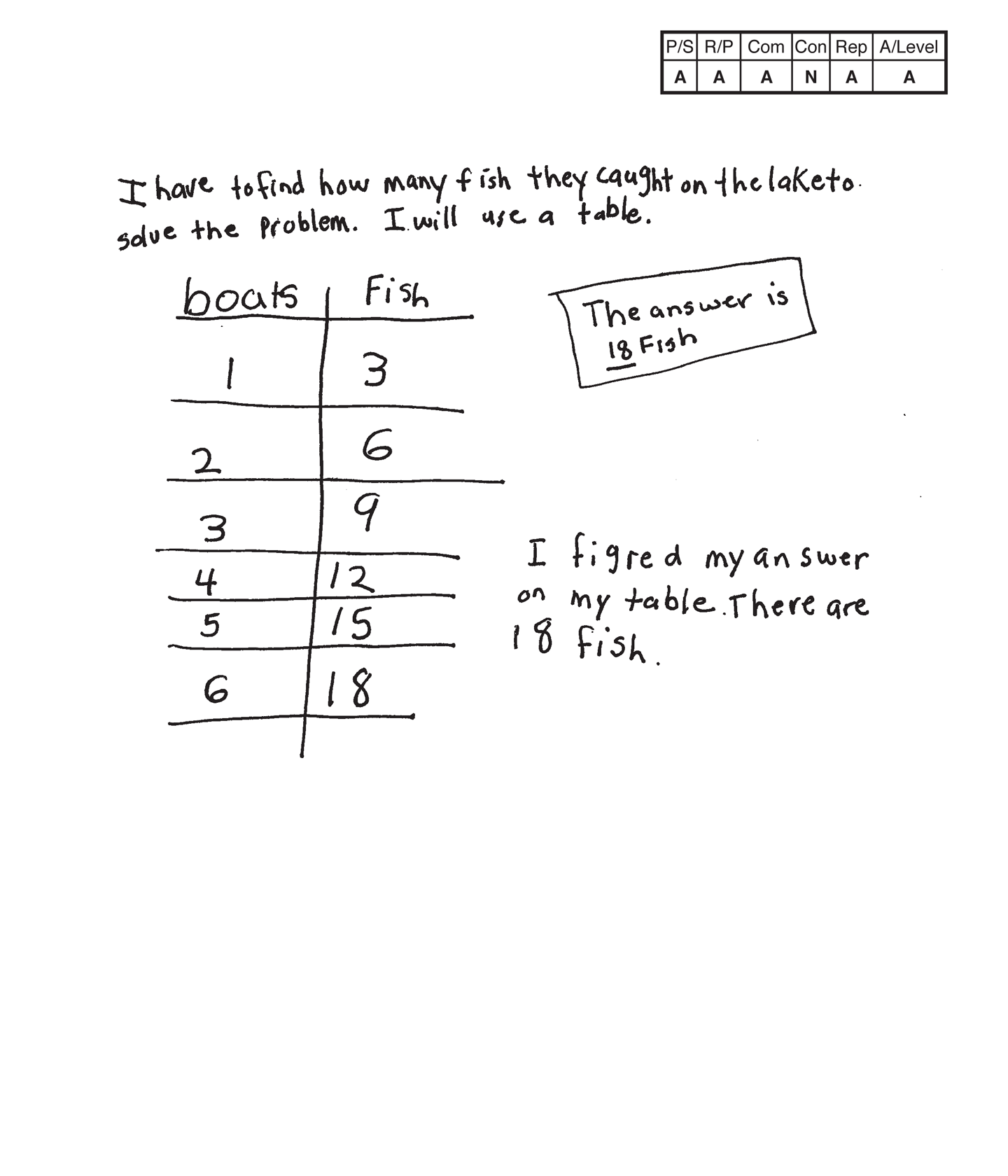
Apprentice 2
Scoring Rationale
Problem Solving
Apprentice
The student's strategy of making a table for boats and fish would work to solve the task but the fish column only represents the fish caught by one friend per boat and not two friends per boat. The student’s answer, "The answer is 18 fish," is incorrect.
Reasoning & Proof
Apprentice
The student has a flaw in their reasoning. The running total of fish in the second column in the student's table only represents three fish per friend and not six fish for two friends.
Communication
Apprentice
The student correctly uses the mathematical term table.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Apprentice
The student's table is appropriate but not accurate. The fish column has incorrect data. The data should represent 6, 12, 18, 24, 30, 36 fish.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for "Using the Assessment Rubric."
Practitioner
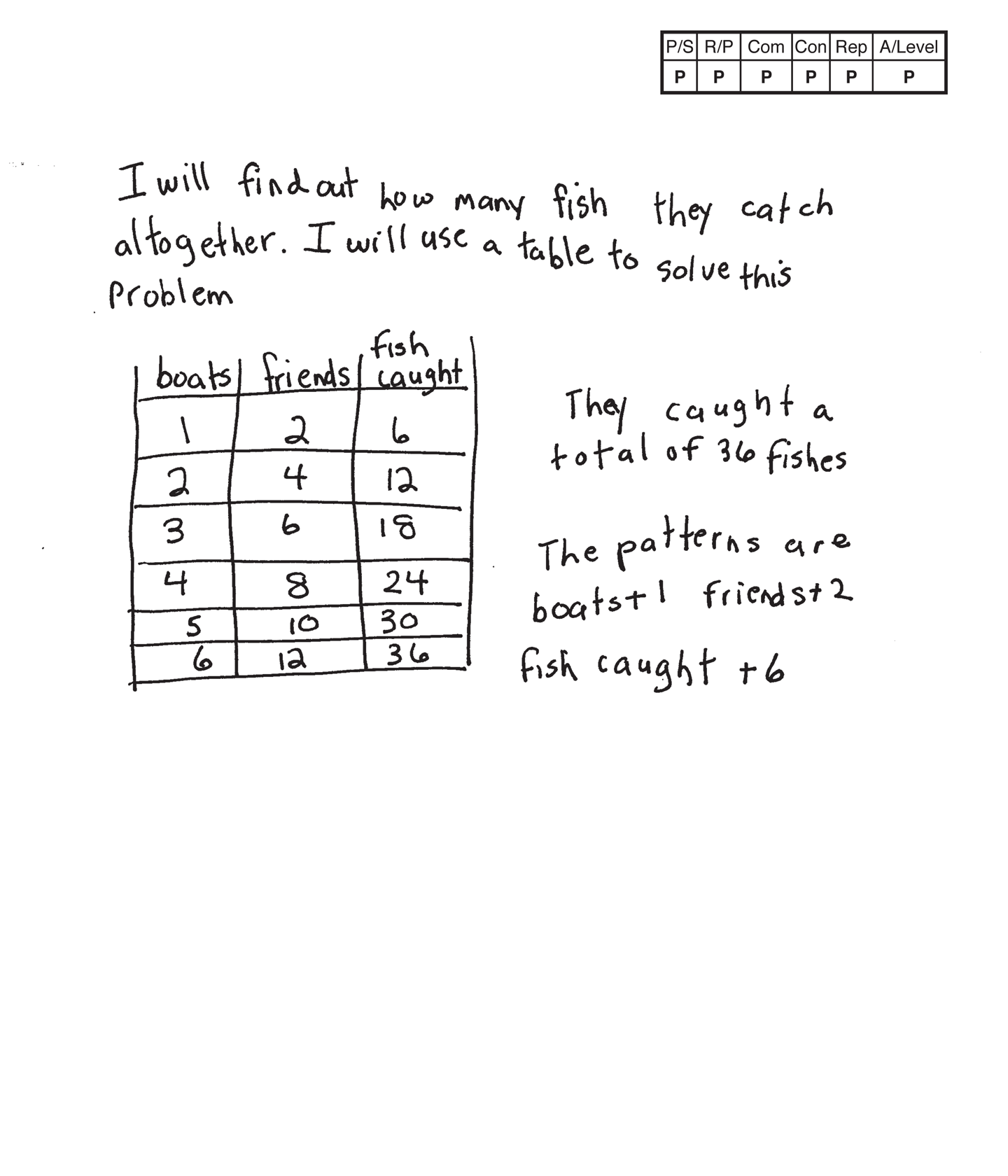
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a table to show six boats, two people, and a running total of fish caught would work to solve the task. The student states a correct answer, "They caught a total of 36 fishes."
Reasoning & Proof
Practitioner
The student provides adequate evidence of their reasoning both in their table and text. The student applies understanding of multiplication by applying the counting by one, two, and six patterns.
Communication
Practitioner
The student correctly uses the mathematical terms table, total and pattern.
Connections
Practitioner
The student makes the mathematically relevant observations, "The patterns are boats +1, friends + 2, fish caught +6."
Representation
Practitioner
The student's table is appropriate and accurate. All necessary labels are provided and the data is correct.
Overall Achievement Level:
Practitioner
 ,
,
Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
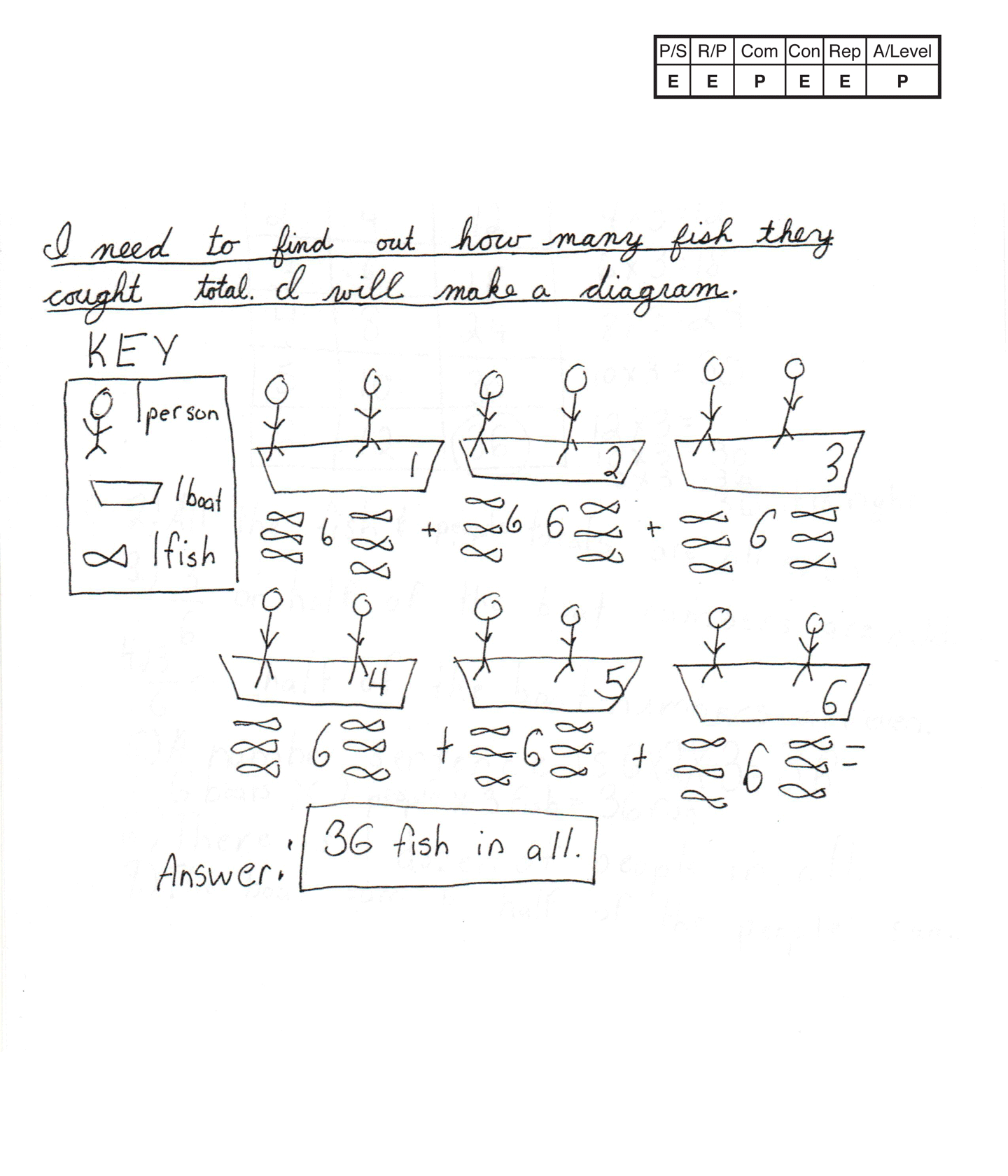
The student's strategy of diagramming the boats, kids, and fish, and providing an accurate key works to solve the task. The student states a correct answer, "36 fish."
Reasoning & Proof
Practitioner
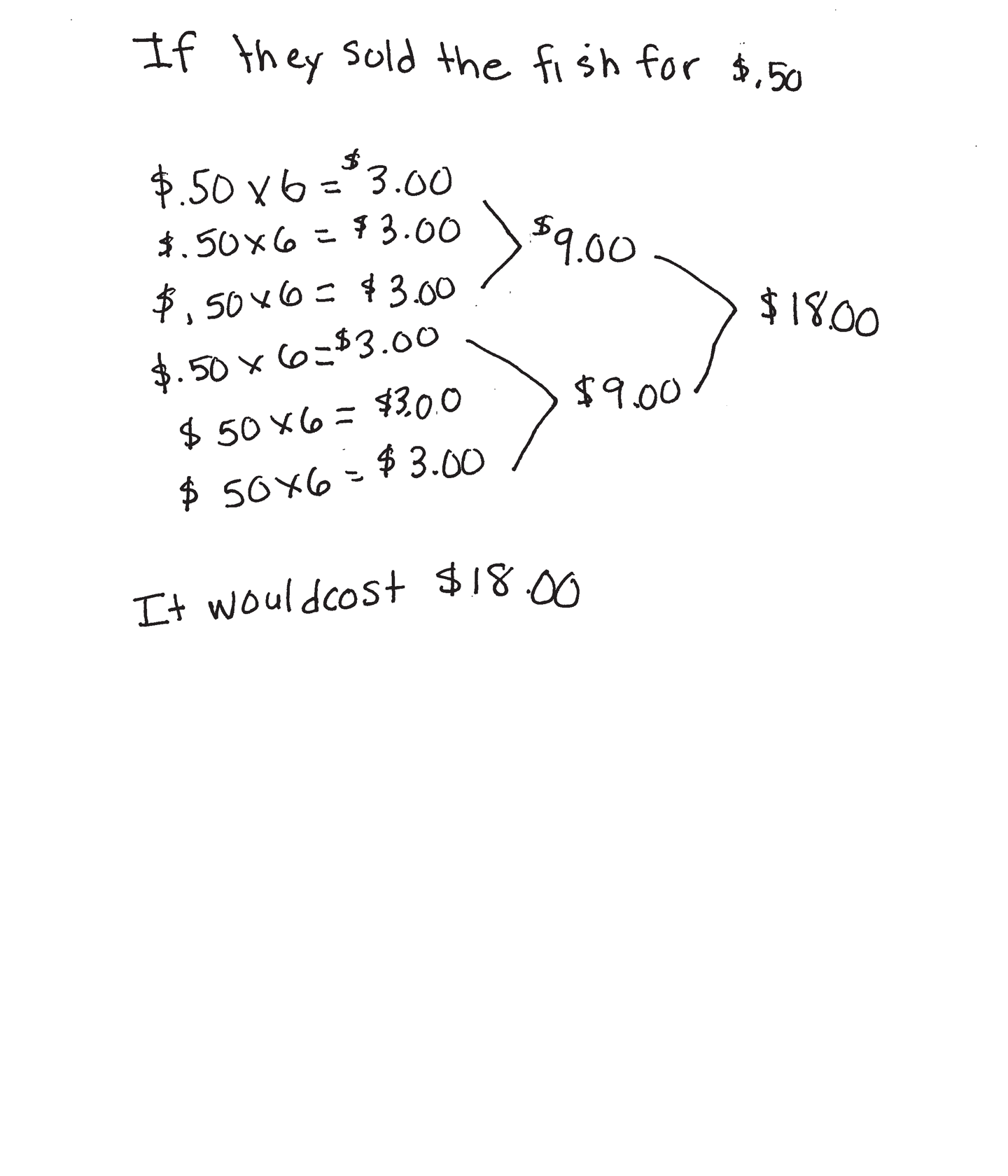
The student demonstrates understanding of the mathematical concept of applying multiplication and patterns to find the total number of fish that can be caught while fishing. The student also applies multiplication and addition in determining the total cost of the 36 fish sold at 50 cents per fish.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, key, pattern, dozen and cost. The student correctly uses the mathematical notation $.50, $3.00, $9.00, $18.00.
Connections
Practitioner
The student makes the mathematically relevant observations, "I saw the add 6 pattern for fish," and, "I saw that there were 12 kids and that is a dozen." The student adds their own part two of the task by determining that if each fish sold for $.50, the total cost would be $18.00.
Representation
Practitioner
The student's diagram is appropriate and accurate. A key is used to represent the boats, kids and fish.
Overall Achievement Level:
Practitioner
 ,
,

Practitioner 3
Scoring Rationale
Problem Solving
Expert
The student's strategy of diagramming the persons, boats, and fish, and providing an accurate key works to solve the task. The student states a correct answer, "36 fish in all." The student verifies their answer by using a table to compare with the data in their diagram.
Reasoning & Proof
Expert
The student demonstrates understanding of the mathematical concept of applying multiplication patterns to find the total number of fish that can be caught while fishing. The student also applies multiplication and addition in a table to verify their answer. The student brings the understanding of fractions to the task.
Communication
Practitioner
The student correctly uses the mathematical terms total, diagram, key, table, even, odd, half, number sentence, dozen, sum. The student correctly uses the mathematical notation `sf (3/6)`. All of these terms are considered typical to the Grade three Common Core standards and do not earn a performance level of Expert.
Connections
Expert
The student makes the mathematically relevant Practitioner connections, "All the fish & people totals are all even," and, "A number sentence is 6 x 2 x 3 = 36. 6 boats x 2 people x 3 fish = 36 fish." The student makes the Expert connection of applying an understanding of fractions to the task. The student states, "`sf (3/6)` or half of the boat numbers are odd," "`sf (3/6)` or half of the boat numbers are even," and "The boat sum is half of the people sum." The student verifies their answer by comparing the data on their diagram with the data on a table and stating, "it is right."
Representation
Expert
The student's diagram is appropriate and accurate. A key is used to represent the persons, boats, and fish. The student's table is appropriate and accurate. All labels are provided and the the entered data is correct. The student compares the data of their diagram and table to help verify that the answer is correct.
Overall Achievement Level:
Practitioner
Expert
 ,
,

Expert 1
Scoring Rationale
Problem Solving
Expert
The student's strategy of using a diagram to determine the total number of fish caught by 12 people works to solve the task. The student's answer, "36 fish were caught," is correct. The student verifies their answer by making a table and equations. The student also verifies their answer by generalizing a rule for finding the total number of fish caught for any number of boats.
Reasoning & Proof
Expert
The student demonstrates correct reasoning of the underlying concepts in the problem. The student uses multiplication correctly. The student generalizes a rule, 6 · b = f, to verify that the data in their table is accurate, the answer is correct, and to find the number of fish for larger numbers of boats.
Communication
Expert
The student correctly uses the mathematical terms diagram, key, table, total, more than, dozen, pattern and rule. The student correctly uses symbolic notation 6 · b = f with the variables "b" and "f" defined in a key.
Connections
Expert
The student makes the Practitioner mathematically relevant observations, "The boat pattern is + 1," "The friends pattern is + 2," "The fish pattern is + 6," "There are more total fish than boats or friends," "36 fish is 3 dozen." The student makes the Expert connection of generalizing a rule, 6 · b = f. The student supplies a key to define the variables, b and f, and states, "Each boat will always have two people in it." The student uses the rule to verify that the data in their table is accurate and states, "I am right because I get 36 fish all the time." The student also uses the rule to find the number of fish for 10 and 50 boats.
Representation
Expert
The student's diagram is appropriate to the problem and accurate. A key is provided to define boat, fish, and person. The student's table is appropriate and accurate with all necessary labels and correctly entered data. The student uses their table to analyze the relationship between the boats and fish to generalize a rule to find the total number of fish for any number of boats.




MP.1
Make sense of problems and persevere in solving them.