Ben's Apple Pie
Ben's mom makes an apple pie. Ben's mom cuts the pie into eight equal pieces. Ben and three friends each eat one piece of apple pie. Ben says they ate one-half of the pie. Brad says they ate four-eighths of the pie. Who is correct? Show all your mathematical thinking.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
A student may independently select a printed number line, number chart, ten frames, graph paper, etc. as they work on a task.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.
Possible Solutions
Assess
Novice

Novice 1
Scoring Rationale
Problem Solving
Novice
The student's strategy of making a diagram (area model) to show eighths of a pie would work to solve this task but the student does not show equivalent slices of pie. The student's answer, "Brad is correct," is incorrect.
Reasoning & Proof
Novice
The student does not show correct reasoning of the underlying concept of equivalent parts of a whole. Without this understanding, the student cannot solve this task correctly. The student also states, "mom didn't cut it into halfs," which is incorrect reasoning. The student does not understand that the task is requiring the student to compare two fractions.
Communication
Apprentice
The student correctly uses the mathematical term diagram. The student does not earn credit for the term eighths, because the pie is not correctly cut into eight equal pieces. The student also does not earn credit for the term "halfs" because they do not address halves.
Connections
Novice
The student solves the task and stops without making a mathematical connection.
Representation
Apprentice
The student's diagram (area model) is appropriate to the problem but not accurate. The pie is not divided into eight equivalent pieces.
Overall Achievement Level:
Novice

Novice 2
Scoring Rationale
Problem Solving
Novice
The student's strategy of making diagrams (area models) to show eighths of a pie would work to solve this task, but the student does not label the slices correctly. The student's answer, "Ben and Brad are both right," is not correct because this answer is based on area models that, although two are correctly shaded in halves, have incorrect labels. The student's solution has to support a correct answer.
Reasoning & Proof
Novice
The student does not show correct reasoning of how to “read” equivalent parts of a whole. Without this understanding, the student cannot solve this task correctly.
Communication
Apprentice
The student correctly uses the mathematical terms diagram and key. The student does not earn credit for the term "nineths", because the pie is not correctly labeled or cut into nine equal pieces. The student correctly uses the mathematical notation 1/8. (The student was able to correctly label an eighth in the third diagram).
Connections
Apprentice
The student attempts two connections. The first is not correct because the student states, "I did them just like I did these." Since the student's solution for Ben's Apple Pie is incorrect, it cannot be compared to Pizza Pieces. The student attempts to recreate the task by using ninths, but the student's diagram is showing eighths.
Representation
Apprentice
The student's diagrams (area models) are appropriate to the task but not accurate. The labels in all the diagrams are not accurate, two diagrams do not show 1/2, 4/8 shaded, and the diagram used in the student's connection does not represent ninths accurately.
Overall Achievement Level:
Novice
Apprentice

Apprentice 1
Scoring Rationale
Problem Solving
Apprentice
The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten would work to solve this task, but the student did not compare 1/2 to 4/8. The student's answer, "Brad is correct because it says that Bens mom cut the Pie in to eight equal pieces not 2 equal pieces," is not correct.
Reasoning & Proof
Apprentice
The student shows some correct reasoning. The student correctly diagrams how a pie can be cut into eight equal pieces and two equal pieces. The student does not show correct understanding of comparing the two equivalent fractions. The student incorrectly thinks that since mom cut the pie into eight equal pieces you can only consider eighths of a pie.
Communication
Practitioner
The student correctly uses the mathematical term equal from the task. The student also correctly uses the mathematical notation 1/2, 4/8, 1/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.
Connections
Novice
The student solves the task and stops without making a mathematical connection.
Representation
Practitioner
The student's area models are appropriate to the task and are accurate. All necessary labels are included.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for “Using the Assessment Rubric.”
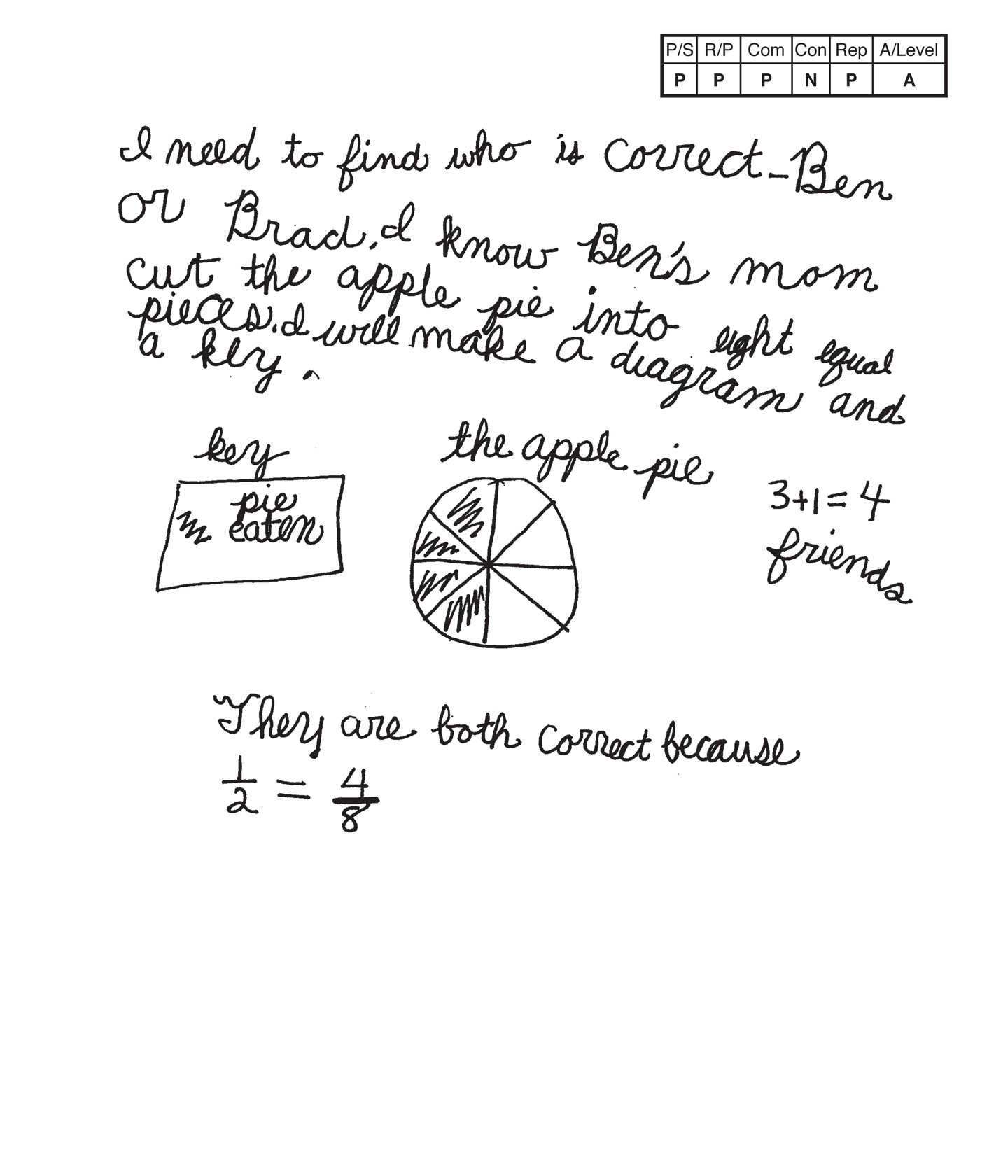
Apprentice 2
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a diagram (area model) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "They are both correct because 1/2 = 4/8," is correct.
Reasoning & Proof
Practitioner
The student shows correct reasoning. The student correctly diagrams how a pie can be cut into eight equal pieces and notes how 4/8 equals 1/2.
Communication
Practitioner
The student correctly uses the mathematical term equal from the task. The student correctly uses the mathematical terms diagram and key. The student also correctly uses the mathematical notation 1/2, 4/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.
Connections
Novice
The student solves the task and stops without making a mathematical connection.
Representation
Practitioner
The student's diagram (area model) is appropriate to the task and accurate. A title is provided and a key defines the amount of pie eaten.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for “Using the Assessment Rubric.”
Practitioner
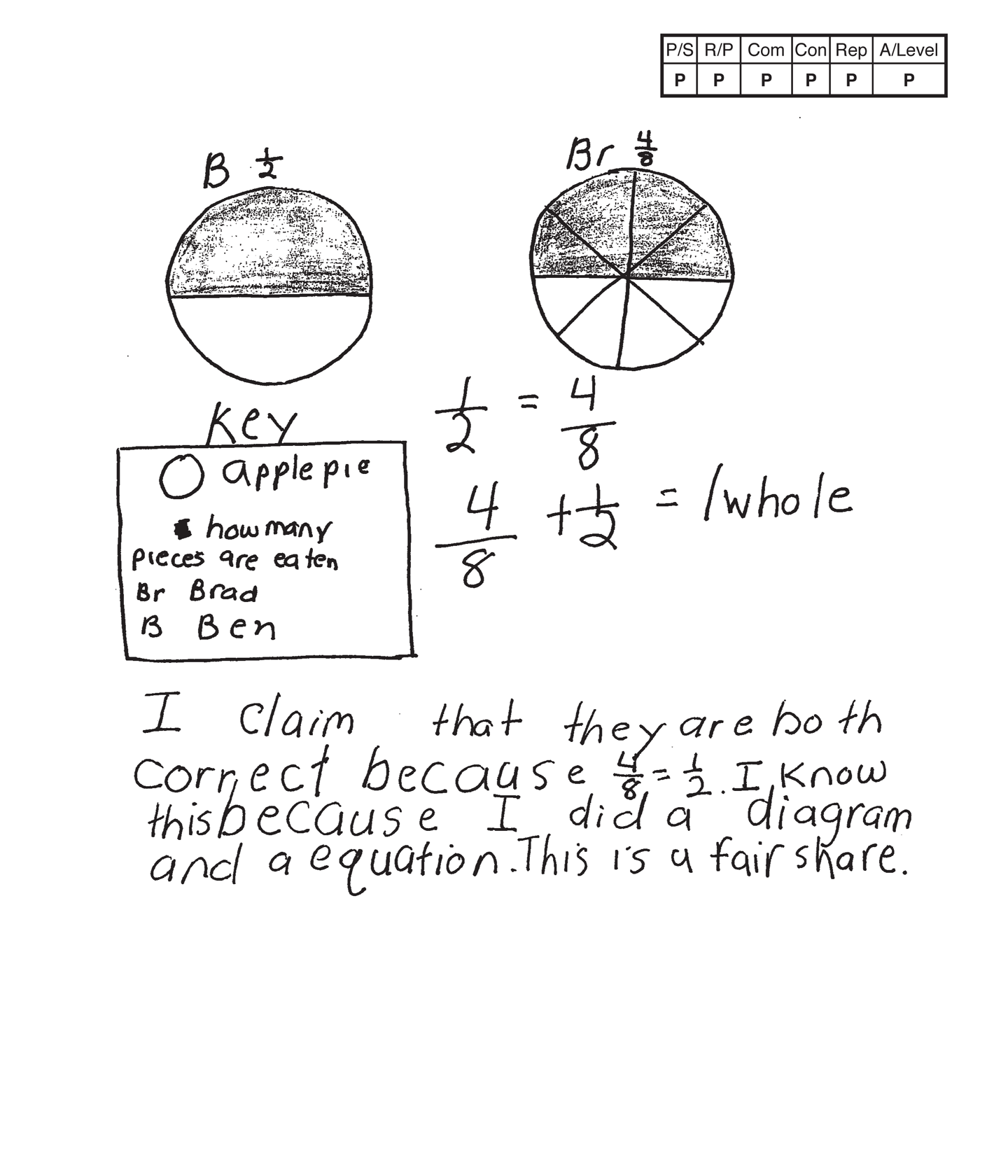 ,
, 
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "I claim that they are both correct because 4/8 = 1/2," is correct.
Reasoning & Proof
Practitioner
The student demonstrates understanding of the underlying concept of comparing two fractions in their area models and text.
Communication
Practitioner
The student correctly uses the mathematical terms key, whole, diagram, equation, fair share and more. The student correctly uses the mathematical notation 1/2, 4/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.
Connections
Practitioner
The student makes the mathematical observations, "This is a fair share," and, "There is 1/2 pie left so they can all have 1 more piece."
Representation
Practitioner
Each of the student's diagrams is appropriate and accurate. A key defines the labels and how many pieces are eaten.
Overall Achievement Level:
Practitioner
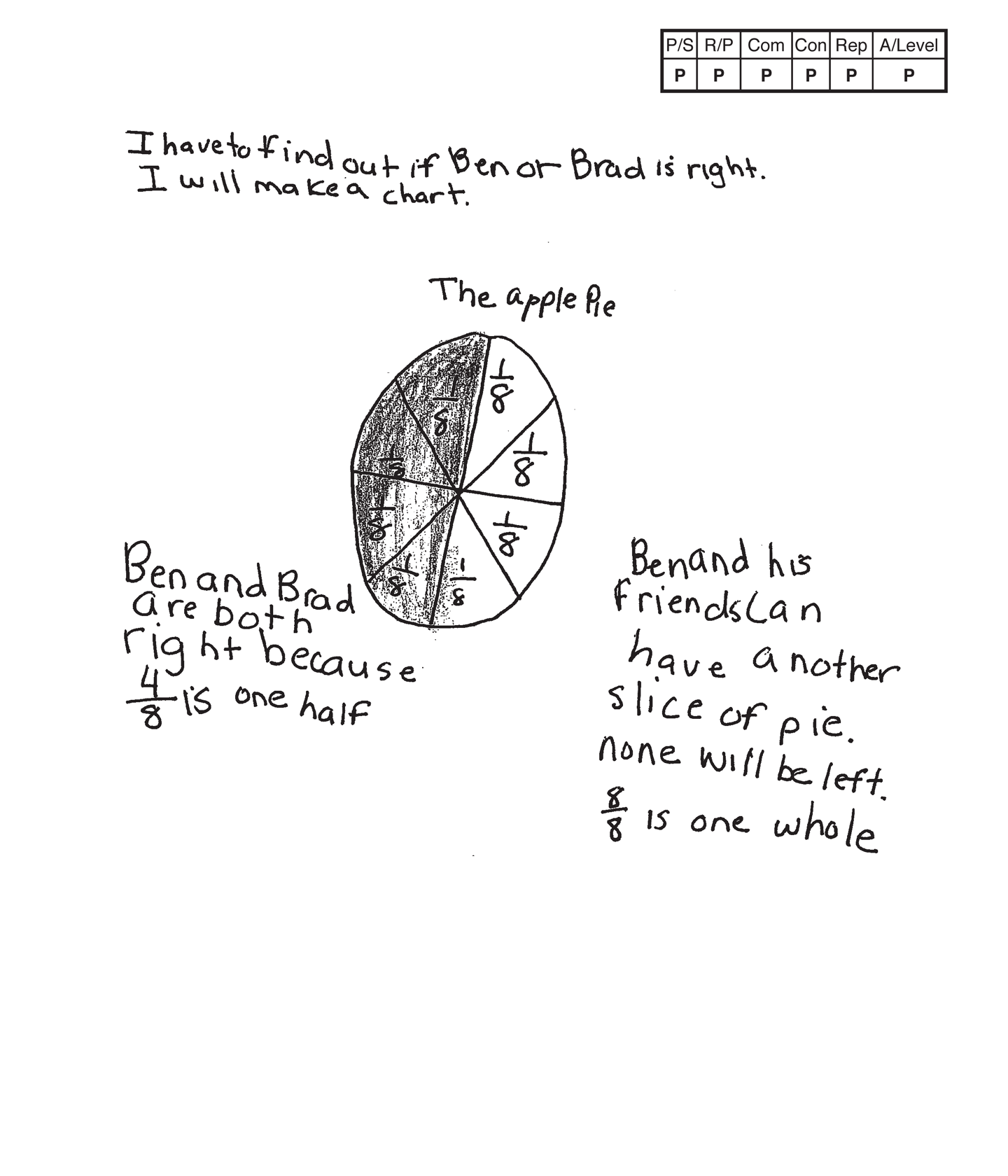
Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making an area model to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "Ben and Brad are both right because 4/8 is one half," is correct.
Reasoning & Proof
Practitioner
The student demonstrates understanding of the underlying concepts of understanding fractional parts of a whole and comparing two fractions in their area model and text.
Communication
Practitioner
The student correctly uses the mathematical term one-half from the task. The student also correctly uses the mathematical term whole. The student correctly uses the mathematical notation 1/8, 4/8, 8/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator. The student does not earn credit for the term chart, because a chart was not included in the student's solution.
Connections
Practitioner
The student makes the mathematical observations, "Ben and his friends Can have another slice of pie. none will be left," and, "8/8 is one whole."
Representation
Practitioner
The student's area model is appropriate to the task and accurate. A title is provided and each slice of pie is labeled 1/8. The student's text supports why the student decides to only notate eighths of the apple pie.
Overall Achievement Level:
Practitioner
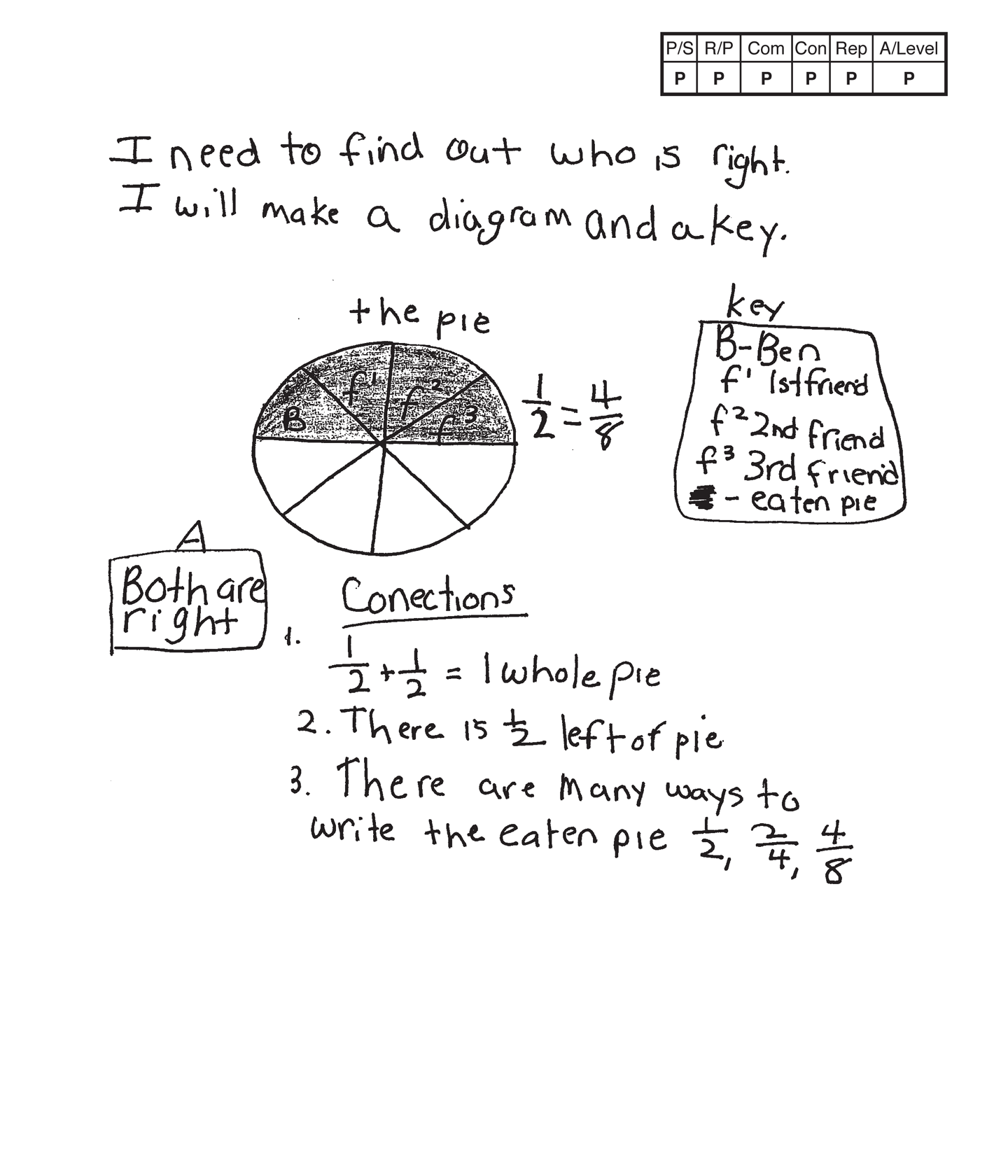
Practitioner 3
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a diagram (area model) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "Both are right," is correct.
Reasoning & Proof
Practitioner
The student demonstrates understanding of the underlying concept of comparing two fractions in their area model and key.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, key, 1st, 2nd, 3rd and whole. The student also correctly uses the mathematical notation 1/2, 4/8, 2/4. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.
Connections
Practitioner
The student makes the mathematical observations, "1/2 + 1/2 = 1 whole pie," "There is 1/2 left of pie," and, "There are many ways to write the eaten pie 1/2, 2/4, 4/8."
Representation
Practitioner
The student's area model is appropriate to the task and accurate. A title is provided and a key defines the sections of the pie that are labeled.
Overall Achievement Level:
Practitioner
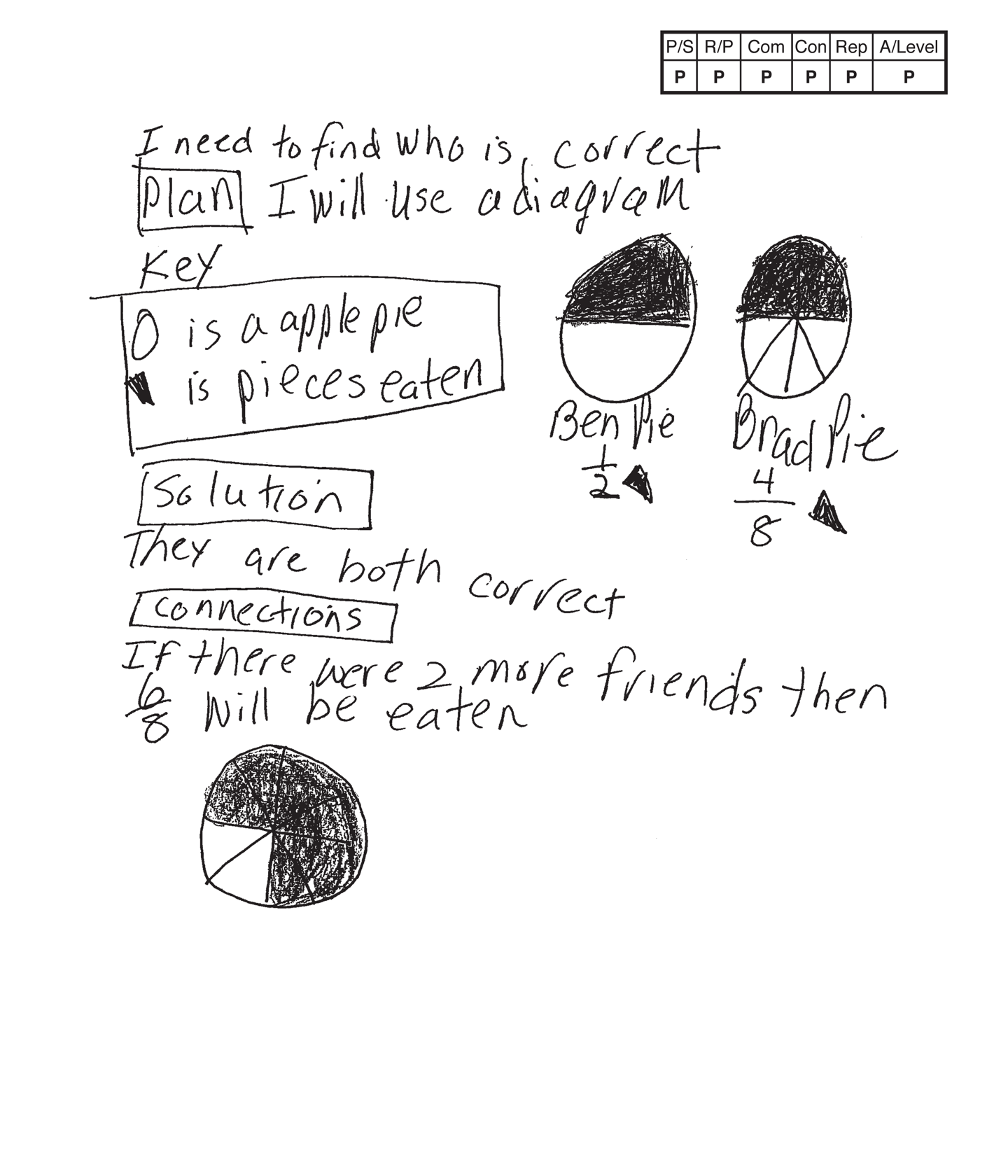
Practitioner 4
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "They are both correct," is correct.
Reasoning & Proof
Practitioner
The student demonstrates understanding of the underlying concept of finding halves and eighths and comparing the two fractions in their area models.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, key and more. The student also correctly uses the mathematical notation 1/2, 4/8, 6/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.
Connections
Practitioner
The student makes the mathematical observation, "If there were 2 more friends then 6/8 will be eaten." The student provides an area model to define 6/8.
Representation
Practitioner
The student's area models are appropriate to the task and accurate. A key defines pie and the sections of the pie that are eaten.
Overall Achievement Level:
Practitioner
Expert
 ,
, 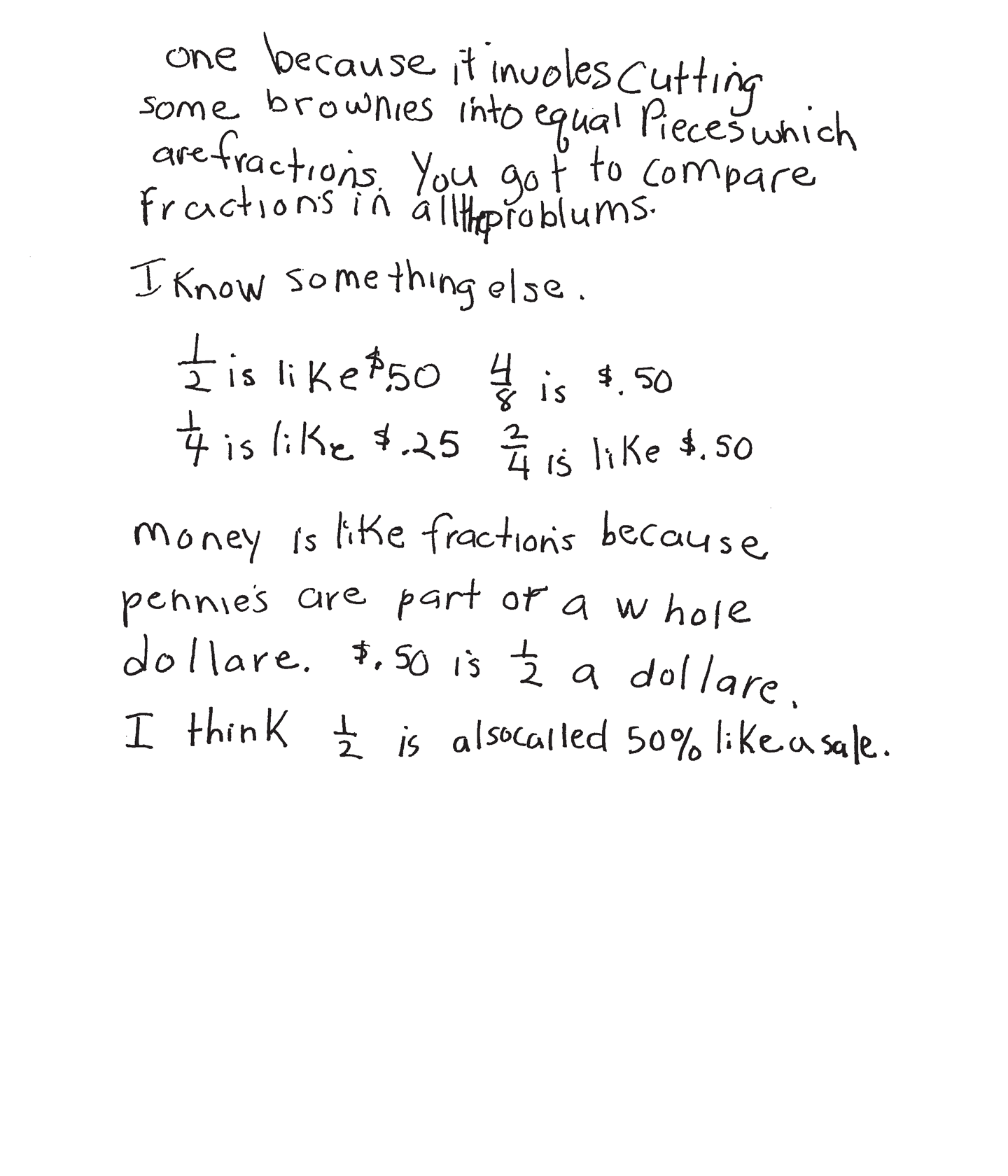
Expert 1
Scoring Rationale
Problem Solving
Expert
The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "Ben and Brad are both right," is correct. The student indicates an understanding of area and analyzes how fractions can be compared to money.
Reasoning & Proof
Expert
The student demonstrates understanding of the underlying concept of comparing two fractions. The student also relates this task to two other problems and links the similar underlying mathematical concepts.
Communication
Expert
The student correctly uses the mathematical term equal from the task. The student also correctly uses the mathematical terms diagram, key, area, amount, fractions, money, pennies, whole, "dollare" (dollar).The student correctly uses the mathematical notation 1/2, 4/8, 1/4, 2/4, $.50, $.25, 50%.
Connections
Expert
The student states, "It is the same area of pie that they eat." The student relates this task to two similar tasks. "This is like the Pizza Pieces problum because Emily and Tara both had the same amount but used diferint fractions. This is also like the brownie one because it involes cutting some brownies into equal Pieces which are fractions. You got to compare fractions in all the problums." The student compares fractions to money and states, "money is like fractions because pennies are part of a whole dollare." The student also states, "1/2 is also called 50% like a sale."
Representation
Expert
Each of the student's diagrams is appropriate and accurate. The student uses the diagrams to note area and to find other equivalent fractions.



MP.1
Make sense of problems and persevere in solving them.