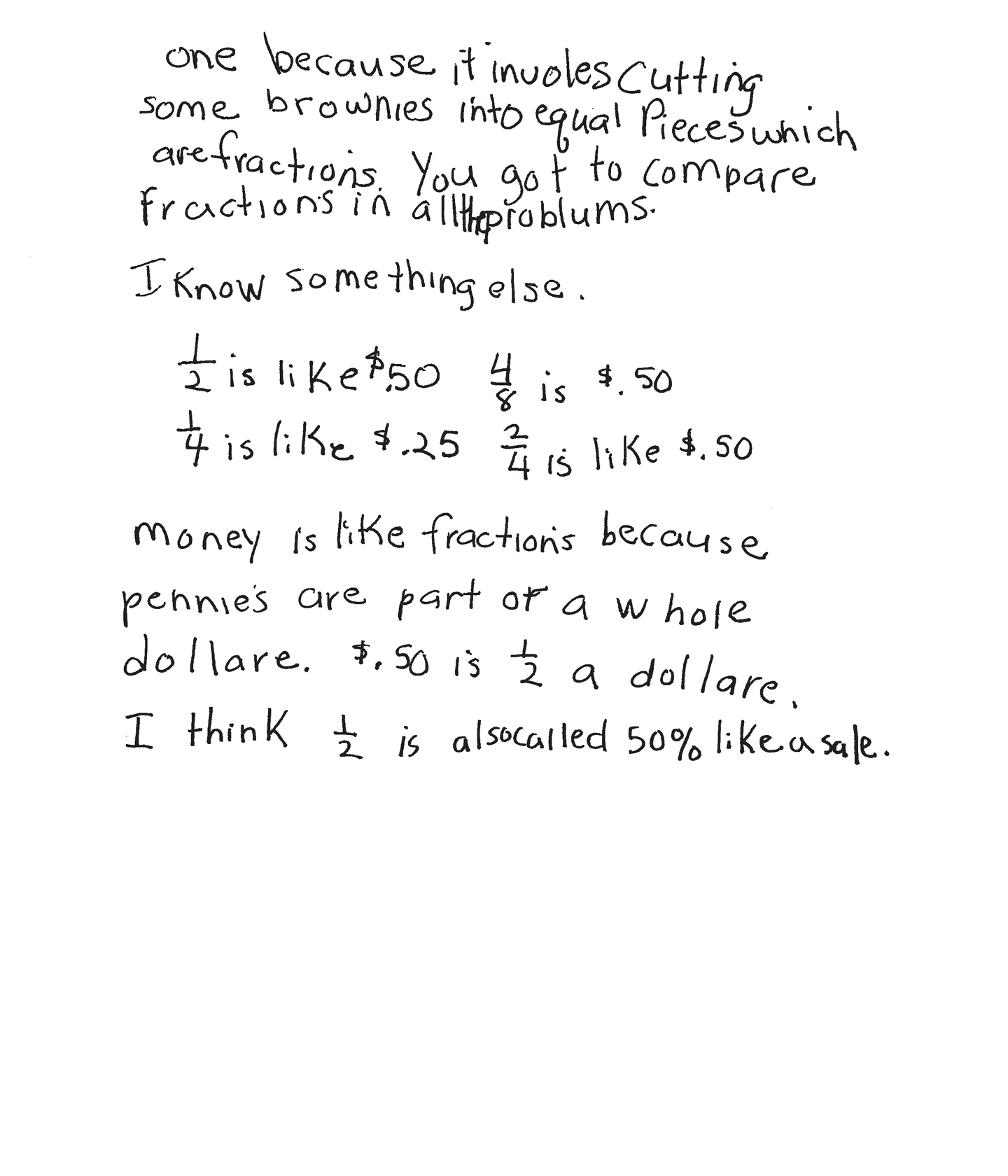Anchor paper 91

Overall Achievement Level:

expert

Student Number:

Anchor Papers:

Problem Solving

expert

Problem Solving Rationale

The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "Ben and Brad are both right," is correct. The student indicates an understanding of area and analyzes how fractions can be compared to money.

Reasoning and Proof

expert

Reasoning Proof Rationale

The student demonstrates understanding of the underlying concept of comparing two fractions. The student also relates this task to two other problems and links the similar underlying mathematical concepts.

Communication Level

expert

Communication Rationale

The student correctly uses the mathematical term equal from the task. The student also correctly uses the mathematical terms diagram, key, area, amount, fractions, money, pennies, whole, "dollare" (dollar).The student correctly uses the mathematical notation 1/2, 4/8, 1/4, 2/4, $.50, $.25, 50%.

Connections Level

expert

Connections RationaleAnchor paper 91

The student states, "It is the same area of pie that they eat." The student relates this task to two similar tasks. "This is like the Pizza Pieces problum because Emily and Tara both had the same amount but used diferint fractions. This is also like the brownie one because it involes cutting some brownies into equal Pieces which are fractions. You got to compare fractions in all the problums." The student compares fractions to money and states, "money is like fractions because pennies are part of a whole dollare." The student also states, "1/2 is also called 50% like a sale."

Representation

expert

Representation Rationale

Each of the student's diagrams is appropriate and accurate. The student uses the diagrams to note area and to find other equivalent fractions.