Anchor paper 87
Problem Solving
practitioner
Problem Solving Rationale
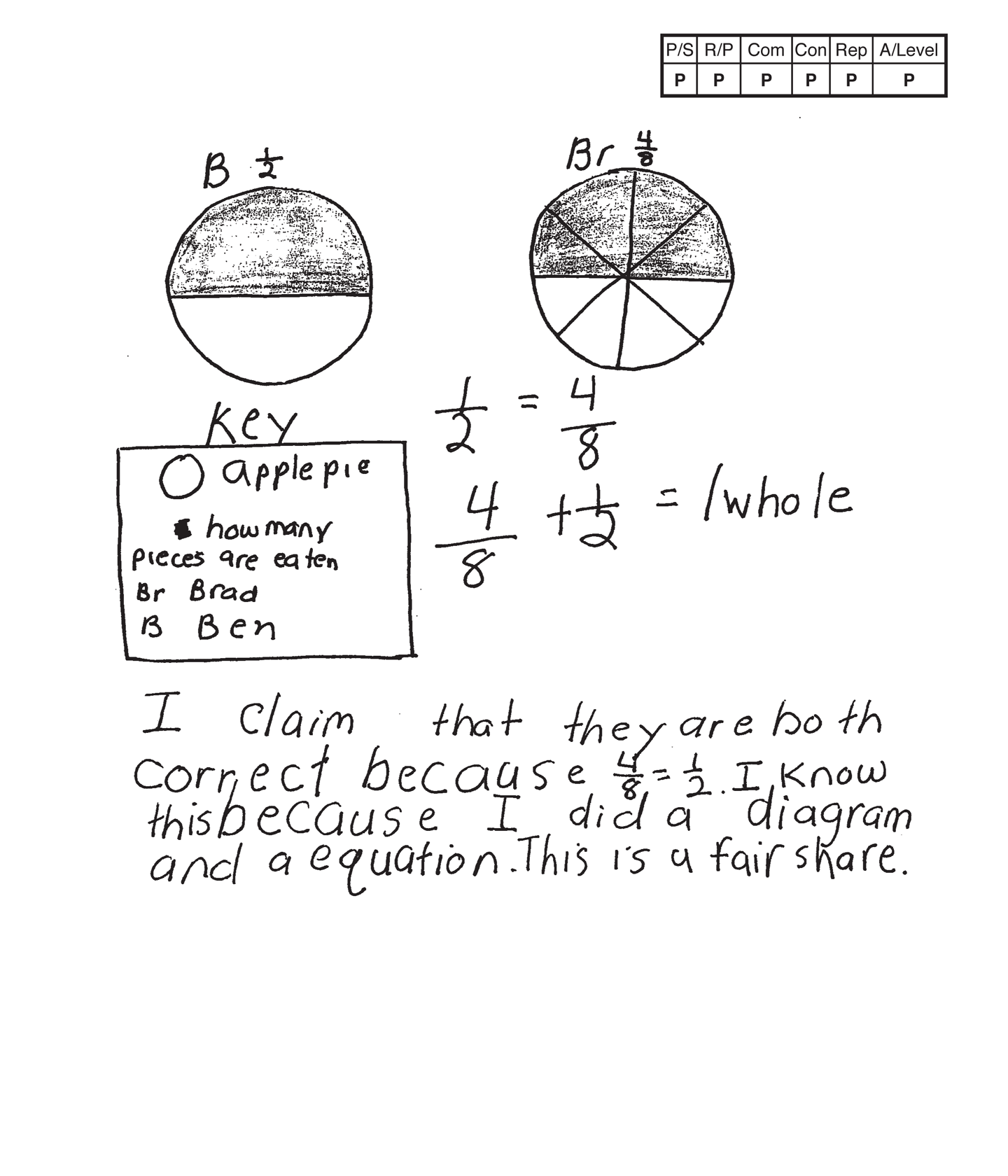
<p>The student's strategy of making diagrams (area models) to determine if 1/2 of a pie eaten is the same as 4/8 of a pie eaten works to solve this task. The student's answer, "I claim that they are both correct because 4/8 = 1/2," is correct.</p>
Reasoning and Proof
practitioner
Reasoning Proof Rationale
<p>The student demonstrates understanding of the underlying concept of comparing two fractions in their area models and text.</p>
Communication Level
practitioner
Communication Rationale
<p>The student correctly uses the mathematical terms <i>key</i>, <i>whole</i>, <i>diagram</i>, <i>equation</i>, <i>fair share</i> and <i>more</i>. The student correctly uses the mathematical notation 1/2, 4/8. Mathematical notation of fractions is different from the written form because the student has to determine the correct numerator and denominator.</p>
Connections Level
practitioner
Connections RationaleAnchor paper 87
<p>The student makes the mathematical observations, "This is a fair share," and, "There is 1/2 pie left so they can all have 1 more piece."</p>
Representation
practitioner
Representation Rationale
<p>Each of the student's diagrams is appropriate and accurate. A key defines the labels and how many pieces are eaten.</p>