Going Airborne

Peter Pan, Aladdin and the Wicked Witch are debating who can fly faster. To settle the dispute they have decided to have a race around the world. The Jolly Organization for Kartoon Exercise has agreed to monitor the event for fairness and sportsmanship.

After `sf text (1)/sf text (2)` an hour, Peter Pan had traveled `sf text (2)/sf text (7)` of the distance around the world.

After `sf text (2)/sf text (5)` of an hour, Aladdin had traveled `sf text (1)/sf text (4)` of the distance around the world.

After `sf text (1)/sf text (3)` of an hour, the Wicked Witch had traveled `sf text (2)/sf text (9)` of the distance around the world.

If these athletic cartoons maintain their current speed, who do you predict will make it around the world first? Be sure to provide a clear mathematically supported argument to the Jolly Organization for Kartoon Exercise.

Printer-Friendly Overhead ○

Assessment

Add Task to Google Classroom

Plan

Underlying Mathematical Concepts

Possible Problem-Solving Strategies

Formal Mathematical Language and Symbolic Notation

Teacher Notes

Possible Teaching Tips:

Teachers need to help students recognize that this is a rate problem. In essence, this is a speed problem. Speed is defined as Distance ÷ Time. By dividing the distance each character has traveled by the time it took, students can find a unit rate for how far each character travels per hour.

Suggested materials

Engagement Image:

Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.

Printer-Friendly Planning Sheet

Printer-Friendly Exemplars Rubric

Possible Solutions

Solutions tabs

Task Solution

If the cartoons maintain their current speed, the Wicked Witch is expected to make it around the world first and win the race.

Two different unit rates can be used to solve this problem: the distance around the world per hour or time per trip around the world.

Unit Rate - Distance around the world per hour

Peter Pan: `sf text(4)/sf text(7)` of the Distance Around the World Per Hour
(`sf text(2)/sf text(7)` around the world ÷ `sf text(1)/sf text(2)` hour = `sf text(2)/sf text(7)` x 2 = `sf text(4)/sf text(7)`)

Aladdin: `sf text(5)/sf text(8)` of the Distance Around the World Per Hour
(`sf text(1)/sf text(4)` around the world ÷ `sf2/sf5` hour = `sf text(1)/sf text(4)` x `sf text(5)/sf text(2)` = `sf text(5)/sf text(8)`)

Wicked Witch: `sf text(6)/sf text(9)` of the Distance Around the World Per Hour
(`sf text(2)/sf text(9)` around the world ÷ `sf text(1)/sf text(3)` hour = `sf text(2)/sf text(9)` x 3 = `sf text(6)/sf text(9)` = `sf text(2)/sf text(3)`)

The cartoon's rates can all be compared to the benchmark of `sf text(1)/sf text(2)`

Peter Pan: `sf text(1)/sf text(2)` = `sf text(3.5)/sf text(7)` so `sf text(4)/sf text(7)` is half of `sf text(1)/sf text(7)` (or `sf text(1)/sf text(14)`) more than `sf text(1)/sf text(2)`.

Aladdin: `sf text (1)/sf text(2)` = `sf text(4)/sf text(8)` so `sf text(5)/sf text(8)` is `sf text(1)/sf text(8)` more than `sf text(1)/sf text(2)`.

Wicked Witch: `sf text(1)/sf text(2)` = `sf text(1.5)/sf text(3)` so `sf text(2)/sf text(3)` is half of `sf text(1)/sf text(3)` (or `sf text(1)/sf text(6)`) more than `sf text(1)/sf text(2)`.

`sf text(1)/sf text(14)` < `sf text(1)/sf text(8)` < `sf text(1)/sf text(6)` so `sf text(4)/sf text(7)` < `sf text(5)/sf text(8)` < `sf text(6)/sf text(9)`

An open number line can be used to show this relationship:

Peter Pan:

`sf text(2)/sf text(7)` x 2 = `sf text(4)/sf text(7)` of the distance around the world per hour

Aladdin:

`sf text(1)/sf text(4)` x 2 + `sf text(1)/sf text(8)` = `sf text(5)/sf text(8)` of the distance around the world per hour

Wicked Witch:

`sf text(2)/sf text(9)` x 3 = `sf text(6)/sf text(9)` of the distance around the world per hour

Unit Rate - Time to travel around the world once

It will take Peter Pan 1`sf text(3)/sf text(4)` hours to travel around the world
(`sf text(1)/sf text(2)` hour ÷ `sf text(2)/sf text(7)` around the world = `sf text(1)/sf text(2)` x `sf text(7)/sf text(2)` = `sf text(7)/sf text(4)` = 1`sf text(3)/sf text(4)`)

It will take Aladdin 1`sf text(3)/sf text(5)` hours to travel around the world
(`sf text(2)/sf text(5)` hour ÷ `sf text(1)/sf text(4)` around the world = `sf(2/5)` x 4 = `sf text(8)/sf text(5)` = 1`sf text(3)/sf text(5)`)

It will take the Wicked Witch 1`sf text(1)/sf text(3)` hours to travel around the world
(`sf text(1)/sf text(3)` hour ÷ `sf text(2)/sf text(9)` around the world = `sf text(1)/sf text(3)` x `sf text(9)/sf text(2)` = `sf text(9)/sf text(6)` = 1`sf text(3)/sf text(6)`)

Since 1`sf text(3)/sf text(6)` < 1`sf text(3)/sf text(5)` < 1`sf text(3)/sf text(4)` it will take the Wicked Witch the least amount of time to finish the race.

Tape Diagram - Can be used to find and represent each unit rate

Peter Pan:

`sf text(1)/sf text(2)` hour x 3 + `sf text(1)/sf text(4)` hour = 1 `sf text(3)/sf text(4)` hours

Aladdin:

`sf text(2)/sf text(5)` hour x 4 + `sf text(8)/sf text(5)` = 1 `sf text(3)/sf text(5)` hours

Wicked Witch:

`sf text(1)/sf text(3)` hour x 4 + `sf text(1)/sf text(6)` hour = 1`sf text(3)/sf text(6)` hours

Ratio Table

After 2 hours, Peter Pan could travel 1`sf text(1)/sf text(7)` times around the world; Aladdin could travel 1`sf text(1)/sf text(4)` times around the world; the Wicked Witch could travel 1`sf text(3)/sf text(9)` times around the world.

1`sf text(1)/sf text(7)` < 1`sf text(1)/sf text(4)` < 1`sf text(3)/sf text(9)` so the Wicked Witch is the traveling the fastest. A variety of strategies can be used to compare these rates.

Aladdin is traveling faster than Peter Pan because 1`sf text(1)/sf text(4)` > 1`sf text (1)/sf text(7)`.

The Wicked Witch is traveling faster than Aladdin because 1`sf text(3)/sf text(9)` > 1`sf text(1)/sf text(4)`.

Graph

The information given for each character can be graphed as points on a graph as (time, distance) along with the point (0, 0) for each which represents the start of the race.

The two points for each character can be connected with a line. Each character’s speed is represented by the steepness of their line. Since the Wicked Witch’s line is the steepest, she is traveling at the fastest rate.

Scaling

Each characters' time can be scaled up to 1 hour to find how far each character has traveled per hour.

Peter Pan: `sf text(1)/sf text(2)` hour x 2 = 1 hour. `sf text(2)/sf text(7)` of the distance x 2 = `sf text(4)/sf text(7)`.

Aladdin: `sf text(2)/sf text(5)` hour x 2.5 = 1 hour. `sf text(1)/sf text(4)` of the distance x 2.5 = `sf text(2.5)/sf text(4)` or `sf text(5)/sf text(8)`.

Wicked Witch: `sf text(1)/sf text(3)` hour x 3 = 1 hour. `sf text(2)/sf text(9)` of the distance x 3 = `sf text(6)/sf text(9)`.

Printer-friendly Anchor Paper & Scoring Rationales

Assess

Anchor Papers

Printer-friendly Exemplars Rubric

Novice

Apprentice

Practitioner

Expert

This student does not meet the standard.

Novice 1

Scoring Rationale

Problem Solving

Novice

The student’s strategy of changing the hour values to minutes is incomplete and does not lead to a solution. The student states “Peter Pan” which we must assume the student believes is the fastest, which is incorrect.

Reasoning & Proof

Novice

The student does not demonstrate an understanding of the concept of unit rates associated with ratios of fractions. It appears the student attempts to convert fractional parts of hours to minutes. The student does not consider the distances traveled in this solution process. The mathematical reasoning present does not support their conclusion.

Communication

Novice

The student does not communicate any purpose for this problem. Limited math language is provided by the student, (min., hour) but significant interpretation is required to determine where these labels connect. The student provides no explanation of his/her approach and only states “Peter Pan” when giving the solution.

Connections

Novice

The student does not make a mathematically relevant observation.

Representation

Novice

No attempt is made to make a mathematical representation.

Overall Achievement Level:

Novice

This student does not meet the standard.

Apprentice 1

Scoring Rationale

Problem Solving

Practitioner

The student’s initial strategy of finding common denominators to compare the distance traveled for each character (252) could work to solve the task. The student correctly determines that Peter Pan will take 1 hour and 45 minutes to travel around the world, Aladdin will take 1 hour 36 minutes, and the Wicked Witch will take 1 hour 30 minutes and concludes that the Wicked Witch will travel around the world's fastest. However, the strategy used to reach this solution is not evident.

Reasoning & Proof

Apprentice

The student demonstrates some understanding of the concept of unit rates associated with ratios of fractions. The student correctly determines the distance traveled around the world by each character’s first interval using common denominators. The final solution is correct. The student however provides no mathematical justification for his/her conclusions for how much time it would take each character to complete the race.

Communication

Apprentice

The student provides a clear purpose for the problem in his/her opening sentence. The student attempts to explain his/her initial approach of finding common denominators, but the mathematical argument lacks detail and significant interpretation of the required approach. The student does not provide his/her approach to how the time traveled was converted into minutes or how the exact time to travel completely around the world was calculated. The student correctly uses formal math language, including fastest, distance, common denominators, minutes, hour, and constant pace.

Connections

Practitioner

The student identifies an important situational context within the task when he/she states that “this is all assuming that they each of them keep a constant pace.”

Representation

Practitioner

The student constructs a table which accurately portrays his/her solutions to the time and distances traveled by each of the contenders in the problem.

Overall Achievement Level:

Apprentice

This student does not meet the standard.

Apprentice 2

Scoring Rationale

Problem Solving

Apprentice

The student’s strategy of scaling up the fractional amount of distances traveled in a given time to reach a sum of 1 trip around the world to determine how long it takes each character to travel around the world and which character is traveling the fastest could work to solve the task. The student incorrectly organizes the data for Aladdin, switching the values for time and distance, resulting in an incorrect conclusion that Aladdin will complete the trip in the smallest amount of time.

Reasoning & Proof

Apprentice

The student demonstrates some correct understanding of unit rates associated with ratios of fractions. The student uses incorrect reasoning when they defined Aladdin’s ratio of Distance traveled : Time spent traveling, which is the opposite ratio order used for Peter Pan and the Wicked Witch. The student uses repeated addition to scale up the fractional distances traveled by each character to equal one full trip around the world. The values determined for Peter Pan and the Wicked Witch are correct, while Aladdin’s is incorrect.

Communication

Apprentice

The student attempts an organized, sequenced, and labeled response to communicate his/her work. The student explains the steps to the solution process and explicitly states the solution even though it is incorrect. The use of formal math language is limited, yet appropriate. The student uses incorrect symbolic notation when showing the relationship between distance traveled and the time it takes for each of the characters. The student shows this relationship as `sf text (2)/sf text (7)` = `sf text (1)/sf text (2)` instead of `sf text (2)/sf text (7)` : `sf text (1)/sf text (2)`. The student inconsistently includes labels for units of measure (distance, hours, minutes).

Connections

Apprentice

The student explores the use of rates within the task with additional opportunities to utilize rates to make mathematically based decisions concerning speed of airplanes and the cost of travel.

Representation

Apprentice

The student attempts to organize the data in a grid for the story and his/her calculations. No categories for the table are provided. The relationships between distances traveled and elapsed time are written incorrectly (ex. `sf text(2)/sf text (7)` = `sf text (1)/sf text(2)` instead of `sf text (2)/sf text(7)` : `sf text (1)/sf text(2)`). Unit labels (ex. hours, distance) are missing throughout.

Overall Achievement Level:

Apprentice

This student meets the standard.

Practitioner 1

Scoring Rationale

Problem Solving

Practitioner

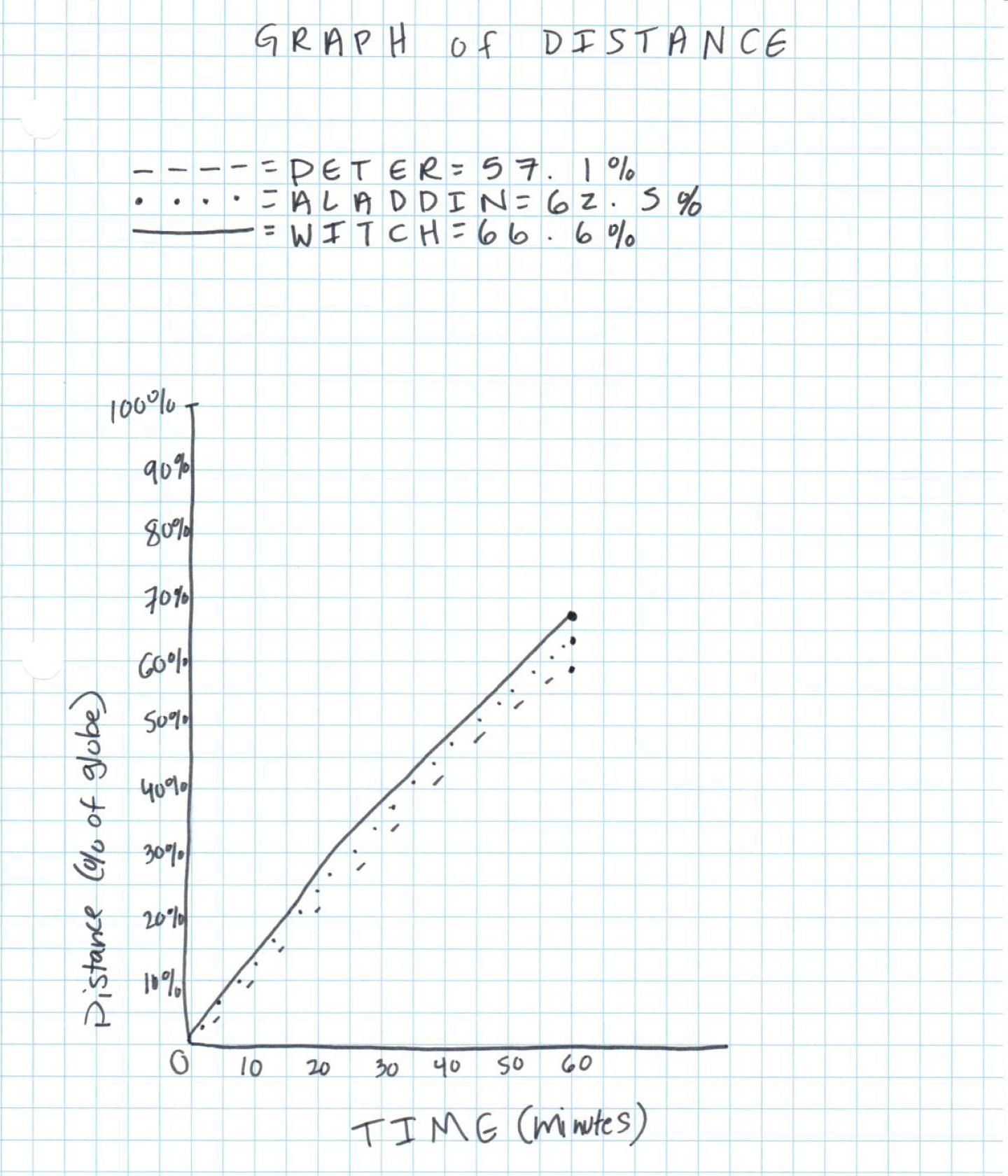
The student’s strategy of scaling up the time traveled to one hour and scaling up the distance traveled per hour by each contender works to solve the problem. The student’s answer “The witch will win, because she is going `sf(0.bar6)`dph, which is faster than the other contestants” is correct.

Reasoning & Proof

Practitioner

The student demonstrates correct understanding of unit rates associated with ratios of fractions. The student converts the time traveled for each character to an hour and then multiplies the distance traveled by the same scale factor. The student then converts the fractions of the distance around the earth traveled into decimal form to compare each contender. The student’s approach is systematic with mathematical justification for each contestant.

Communication

Practitioner

The student’s communication is organized, coherent, and sequenced. The student identifies the problem to be solved, develops a clear approach, and clearly states his/her conclusion. No interpretation is required. The student utilizes formal mathematical language throughout, including distance, per, fastest, dph, ratios, and constant. The work is clear and easy to follow.

Connections

Practitioner

The student’s connection clarifies the mathematical situation within the task.

Representation

Practitioner

The student’s graph is appropriate for the task and helps portray the solution to the problem. The student clearly defines which line represents each of the characters. All necessary labels are provided.

Overall Achievement Level:

Practitioner

This student meets the standard.

Practitioner 2

Scoring Rationale

Problem Solving

Practitioner

The student’s strategy of scaling up the distance traveled by the same scale factor required to bring the cartoon’s race time to one-hour works to solve the problem. The student correctly finds that Peter Pan completes `sf text (4)/sf text (7)` of the total distance around the world in one hour, Aladdin completes `sf text (2.5)/sf text (4)` of the total distance, and the Wicked Witch completes `sf text (6)/sf text (9)` of the distance. The student converts these values to decimals for comparison and correctly determines that the Wicked Witch is traveling the fastest.

Reasoning & Proof

Practitioner

The student demonstrates correct understanding of unit rates associated with ratios of fractions. The student determines the unit rate of distance traveled per one hour by finding a scale factor which calculates each character’s distance traveled after one hour to compare the distance traveled by the characters. The student then converts fractional amounts to decimal equivalents for this comparison. The calculations are accurate and support the solution given.

Communication

Practitioner

The student uses an organized, sequenced, and label response to communicate his/her work. The student identifies the problem to be solved, "having a race around the world to see who is fastest,” explains the steps to his/her solution process and explicitly states the solution. Formal math language (i.e., scale up, convert, denominator, numerator, compare, decimals, fastest) and symbolic notation are used to consolidate math thinking and to communicate ideas. The work is clear and easy to follow.

Connections

Practitioner

The student converts fractional amounts for distances traveled in an hour by each character to decimals for easier comparison.

Representation

Practitioner

The student uses several tables, including a ratio table to organize the data and his/her computations in each step of the solution process. The values and labels given are accurate.

Overall Achievement Level:

Practitioner

This student exceeds the standard.

Expert 1

Scoring Rationale

Problem Solving

Expert

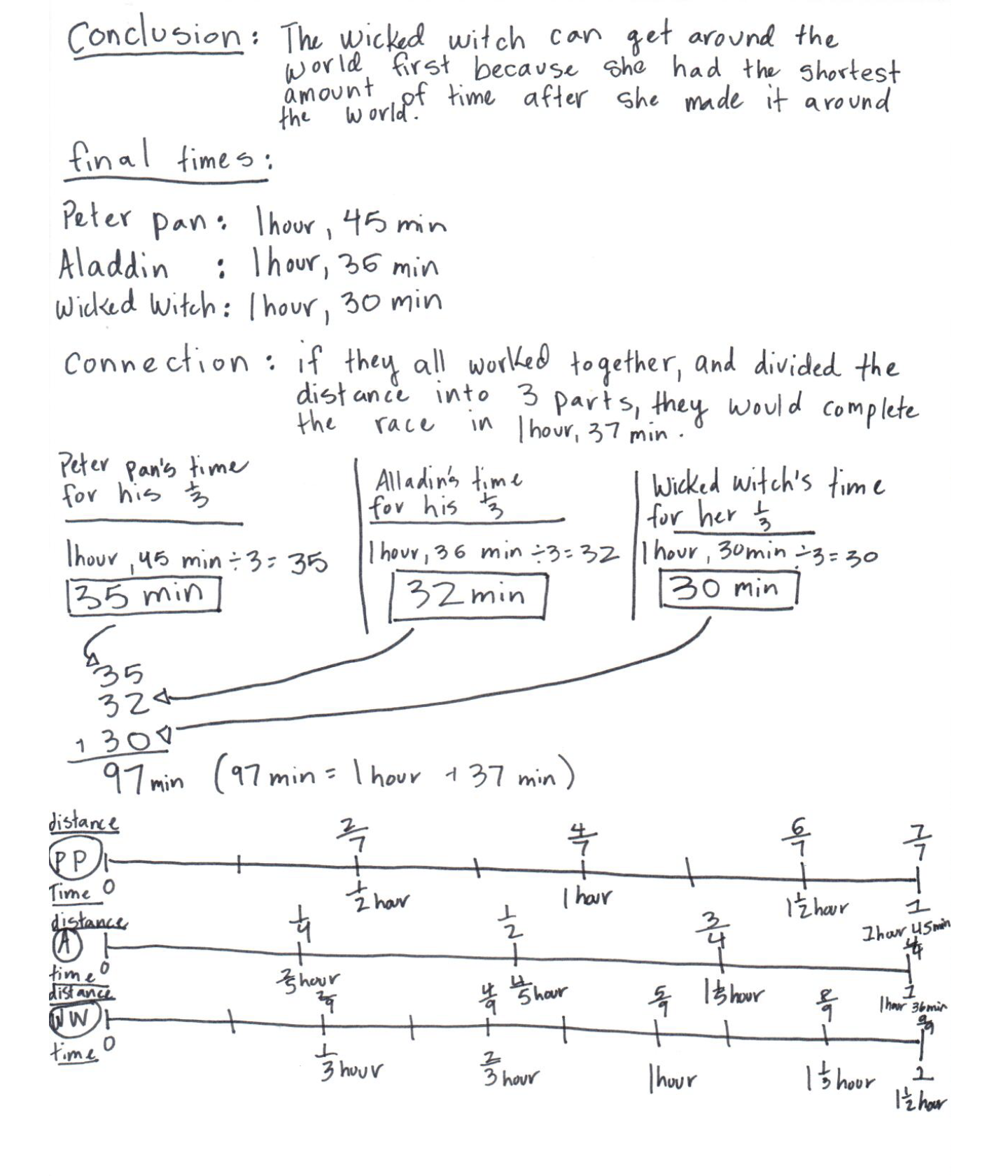
The student’s strategy of scaling up unit fractions to evaluate who will travel around the earth first works to solve this task. The student adjusts this strategy for each of the 3 characters while utilizing this general process. The student correctly determines that it would take Peter Pan 1 hour 45 minutes, Aladdin 1 hour 36 minutes, and the Wicked Witch 1 hour 30 minutes to travel once around the world. The student also utilizes an alternative strategy of double number lines.

Reasoning & Proof

Expert

The student demonstrates correct understanding of unit rates associated with ratios of fractions. The student provides a rigorous mathematical argument to justify his/her conclusion by using double number lines and calculations. Substantial mathematical evidence is developed by the student as he/she converts the distance traveled for Peter Pan and the Wicked Witch into a unit fraction, allowing a scaling up of the time required to complete a trip around the world. The student then converts fractional parts of an hour to minutes. Computations are accurate and support the solution given.

Communication

Expert

The student uses an organized, coherent, and labeled response to communicate his/her approach. The student identifies the problem to be solved, explains the steps to the solution process, explicitly states the solution, and verifies the solution by explaining a second solution strategy. The student utilizes mathematical language and symbolic notation to clearly consolidate and communicate the mathematical ideas for solving this task.

Connections

Expert

The student extends his/her solution to a related task, calculating the time it would take if each character took an equal leg of the trip around the world. The student provides significant mathematical justification for his/her conclusion that it would take 1 hour 37 minutes to complete a trip around the world. The student also converts time in fractional parts of an hour into minutes.

Representation

Expert

The student constructs double number lines to extend his/her thinking to analyze the relationship between distance traveled and the time required to travel that distance. The double number lines verify the solution by showing the complete trip around the world and the time required. The data and labels shown are clear and accurate. The student uses a table to organize data on the connection extension of the problem.

Overall Achievement Level:

Expert

This student exceeds the standard.

Expert 2

Scoring Rationale

Problem Solving

Expert

The student’s strategy of using the relationship between distance, rate, and time (D = R x T) to find the unit rate of distance traveled around the world per hour for each character works to solve the task. The student correctly determines that Peter Pan will travel `sf text (4)/sf text(7)` (.57) of the distance around the world in an hour, Aladdin will travel `sf text (5)/sf text (8)` (.625) of the distance in an hour, and the Wicked Witch will travel `sf text (2)/sf text(3)` (`sf(.6bar6)`) of the distance in an hour. The student correctly determines that the Wicked Witch will travel around the world the fastest. The student then uses an alternative to find the time it would take each character to travel around the world.

Reasoning & Proof

Expert

The student demonstrates correct understanding of unit rates associated with ratios of fractions. The student correctly applies the formula of D ÷ T = R to determine the rate (distance traveled per hour) each character is traveling as a fraction of one hour. The student converts fractional amounts to decimals for easier comparison. As an alternative strategy to compare the speed of each character, the student converts the rate per hour to actual time to complete the entire race in hours and minutes. The calculations support the solution given.

Communication

Expert

The student uses an organized, sequenced, and label response to communicate work. The student identifies the problem to be solved, explains the steps to the solution process, and explicitly states the solution. The student verifies his/her solution by explaining a second solution strategy. Formal math language and symbolic notation, including rate, formula, per, and equations is used to consolidate math thinking and to communicate ideas. The work is clear and easy to follow.

Connections

Expert

The student extends his/her solution of the problem by determining who won the race using two strategies. The student also generalizes the solution process for determining the rate of travel with the algebraic equation `sf text(D)/text(T)` = R and the time required to travel the entire distance around the world with the equation `sf text (D)/text(R)` = T.

Representation

Expert

The student utilizes algebraic equations to provide a symbolic representation to analyze the relationships between distance, time, and rate. The student utilizes two algebraic equations `sf text(D)/text(T)` = R and `sf text(D)/text(R)` = T. The student then determines that comparing both rates and times show that the Wicked Witch is the fastest cartoon. Finally, the student constructs double number lines to compare the time that each character needs to complete one trip around the world.