Going Airborne
Problem Solving
expert
Problem Solving Rationale
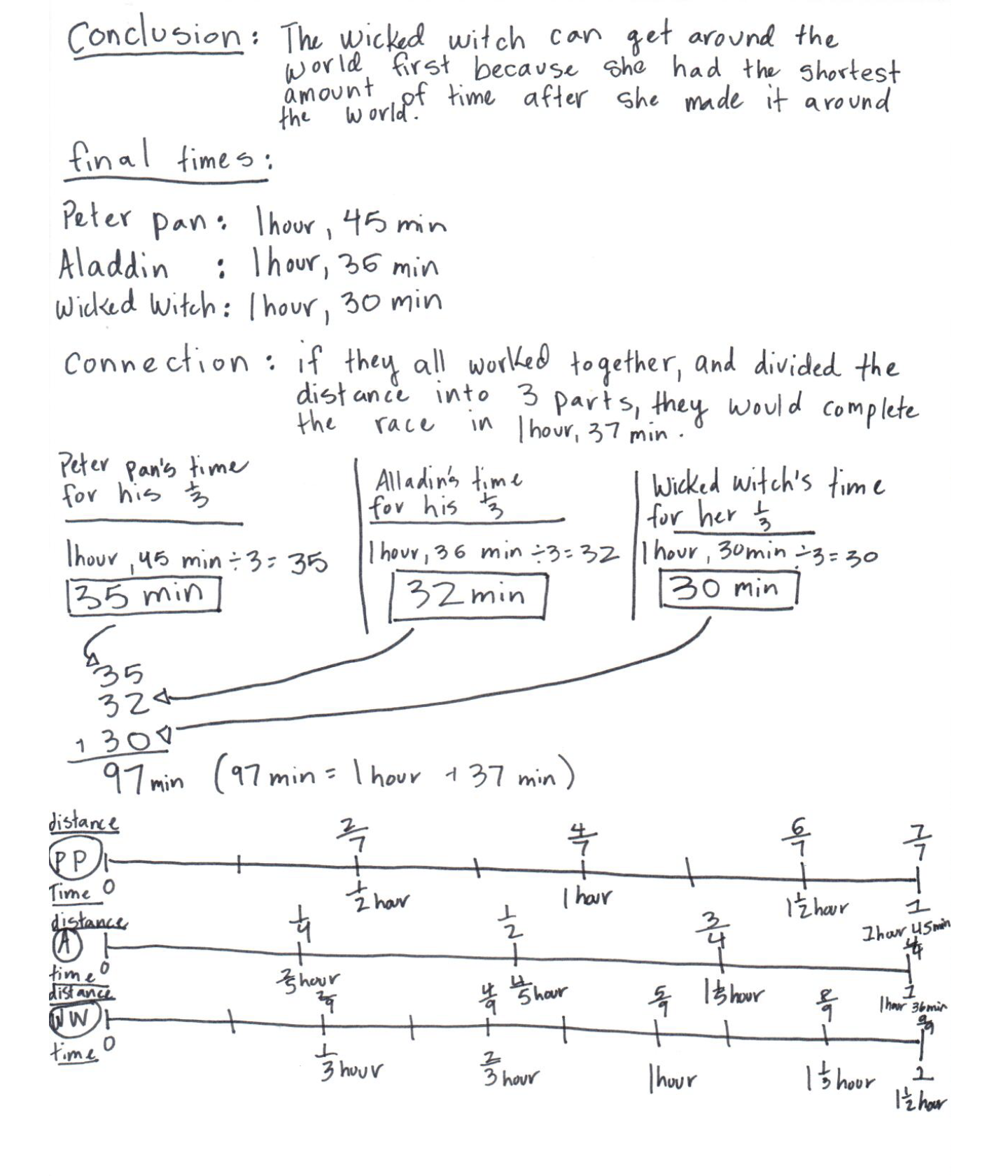
<p>The student’s strategy of scaling up unit fractions to evaluate who will travel around the earth first works to solve this task. The student adjusts this strategy for each of the 3 characters while utilizing this general process. The student correctly determines that it would take Peter Pan 1 hour 45 minutes, Aladdin 1 hour 36 minutes, and the Wicked Witch 1 hour 30 minutes to travel once around the world. The student also utilizes an alternative strategy of double number lines.</p>
Reasoning and Proof
expert
Reasoning Proof Rationale
<p>The student demonstrates correct understanding of unit rates associated with ratios of fractions. The student provides a rigorous mathematical argument to justify his/her conclusion by using double number lines and calculations. Substantial mathematical evidence is developed by the student as he/she converts the distance traveled for Peter Pan and the Wicked Witch into a unit fraction, allowing a scaling up of the time required to complete a trip around the world. The student then converts fractional parts of an hour to minutes. Computations are accurate and support the solution given.</p>
Communication Level
expert
Communication Rationale
<p>The student uses an organized, coherent, and labeled response to communicate his/her approach. The student identifies the problem to be solved, explains the steps to the solution process, explicitly states the solution, and verifies the solution by explaining a second solution strategy. The student utilizes mathematical language and symbolic notation to clearly consolidate and communicate the mathematical ideas for solving this task.</p>
Connections Level
expert
Connections RationaleGoing Airborne
<p>The student extends his/her solution to a related task, calculating the time it would take if each character took an equal leg of the trip around the world. The student provides significant mathematical justification for his/her conclusion that it would take 1 hour 37 minutes to complete a trip around the world. The student also converts time in fractional parts of an hour into minutes.</p>
Representation
expert
Representation Rationale
<p>The student constructs double number lines to extend his/her thinking to analyze the relationship between distance traveled and the time required to travel that distance. The double number lines verify the solution by showing the complete trip around the world and the time required. The data and labels shown are clear and accurate. The student uses a table to organize data on the connection extension of the problem. </p>