Crackers on a Plate
Dad puts ten crackers on a plate.
Alexa eats five crackers.
How many crackers are still on the plate?
Show and tell how you know.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
A student may independently select a printed number line, five/ten frame, place value strips, number chart, ten frame, graph paper, etc. as they work on a task.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.
Possible Solutions
Assess
Novice
Novice 1
Scoring Rationale
Problem Solving
Novice
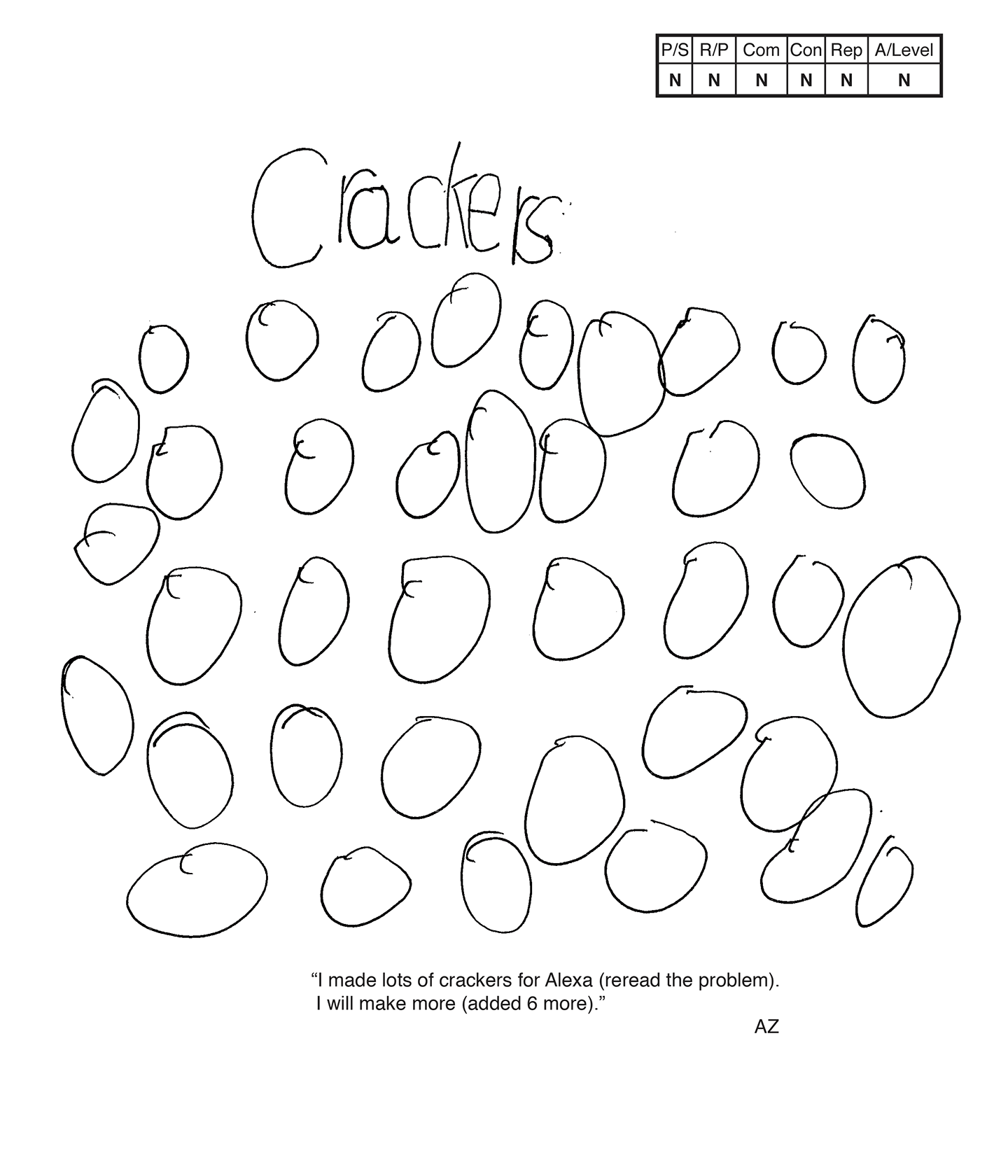
The student's strategy of diagramming numerous crackers for Alexa would not work to solve the task. The student does not state an answer.
Reasoning & Proof
Novice
The student does not show correct reasoning of the underlying concepts of the task. The student does not demonstrate understanding of subtracting five crackers from a total of 10.
Communication
Apprentice
The student correctly uses the mathematical term more.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Novice
The student states "I made lots of crackers for Alexa," and "I will make more." The student does not understand the underlying concepts of the task so is not able to create an appropriate or accurate representation/diagram.
Overall Achievement Level:
Novice
Apprentice

Apprentice 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a diagram of 10 crackers, crossing out five crackers to find five remaining crackers, works to solve this task. The student's answer, "5," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's diagram and scribing supports correct understanding of a set of 10 crackers and subtraction.
Communication
Apprentice
The student correctly uses the mathematical term diagram.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Practitioner
The student's diagram is appropriate to the task and accurate. The scribing defines the crackers.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for “Using the Assessment Rubric.”
Apprentice 2
Scoring Rationale
Problem Solving
Practitioner
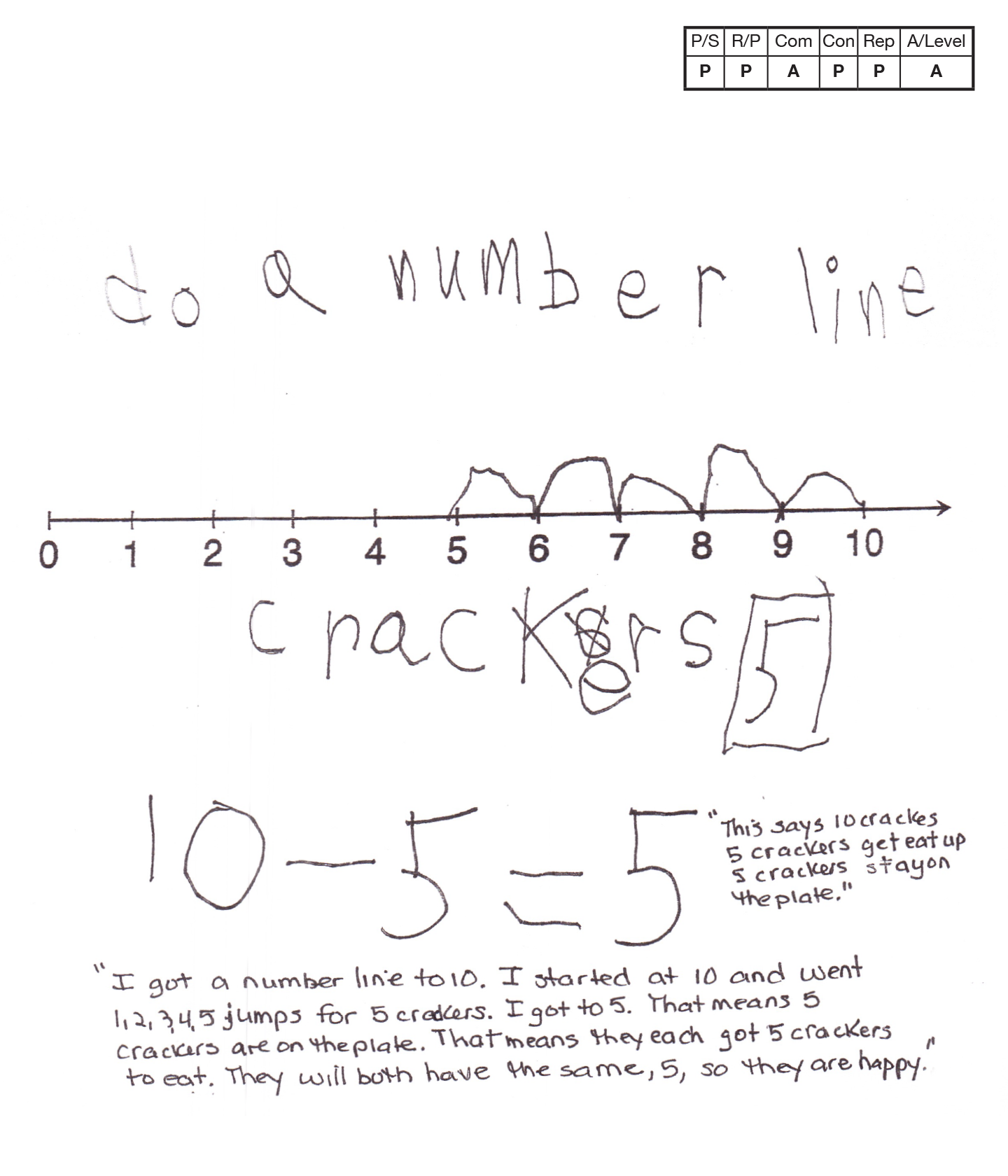
The student's strategy of using a number line to show the ten crackers and how many remain on the plate works to solve the task. The student's answer, "5" is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's number line, equation, and scribing support correct understanding of a set of ten crackers and the need to subtract five crackers.
Communication
Apprentice
The student correctly uses the mathematical term number line.
Connections
Practitioner
The student makes a mathematically relevant observation about their solution. The student states, "They will both have the same, 5, so they are happy."
Note: The student's equation is not considered a connection. It is part of the student's thinking to arrive at five crackers still being on the plate.
Representation
Practitioner
The student's number line is appropriate to the task and accurate. The student provides the label for the crackers. The scribing supports why the student stops at five and that five crackers are still on the plate.
Overall Achievement Level:
Apprentice
Practitioner
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
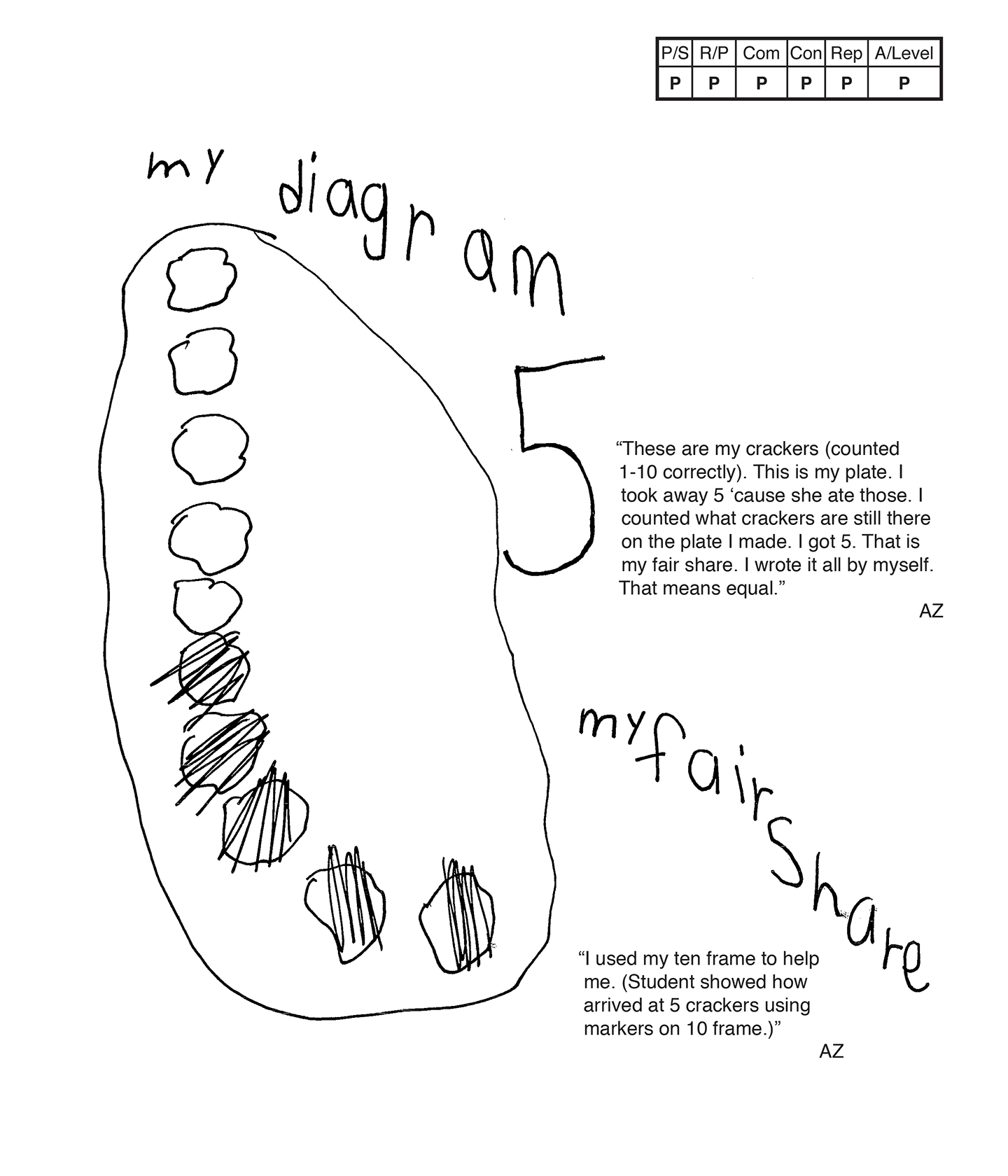
The student's strategy of making a diagram of 10 crackers, crossing out five crackers to find five remaining crackers works, to solve this task. The student's answer, "5," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's diagram and scribing support correct understanding of a set of 10 crackers and subtraction.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, equal, fair share.
Connections
Practitioner
The student places themselves in the task by deciding that the remaining five crackers would be for them. The student states, "I got five. That is my fair share. I wrote it all by myself. That means equal." The teacher notes that the student also used a ten frame and markers to arrive at a correct answer.
Representation
Practitioner
The student's diagram is appropriate to the task and accurate. The scribing defines the crackers.
Overall Achievement Level:
Practitioner

Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a diagram of 10 crackers, crossing out five crackers to find five remaining crackers, and creating a subtraction equation, works to solve this task. The student's answer, "5," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's diagram and scribing support correct understanding of a set of 10 crackers and subtraction.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, key, number.
Connections
Practitioner
The student makes the mathematically relevant observation, "I see she eats five and it is five crackers still on the plate. That is the same number of crackers."
Representation
Practitioner
The student's diagram is appropriate to the task and accurate. A key and the scribing defines the crackers.
Overall Achievement Level:
Practitioner

Practitioner 3
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a ten frame to show the ten crackers and how many remain on the plate after five are eaten works to solve the task. The student's answer, "5" is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's ten frame and scribing support correct understanding of a set of ten crackers and the need to subtract five crackers.
Communication
Practitioner
The student correctly use the mathematical terms 10 frame, diagram.
Connections
Practitioner
The student uses a second strategy, a diagram, to show that five crackers are still on the plate after subtracting the five eaten crackers. The student does not compare the two strategies to earn the Expert level.
Representation
Practitioner
The student's ten frame is appropriate to the task and accurate. The student's scribing defines the crackers. The student's diagram is appropriate to the task and accurate. The student's scribing defines the crackers.
Overall Achievement Level:
Practitioner

Practitioner 4
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a rekenrek to show the ten crackers and how many remain on the plate after five are eaten works to solve the task. The student's answer, "5-plate" is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the underlying concepts of the task. The student's rekenrek, and scribing support correct understanding of a set of ten crackers and the need to subtract five crackers for a difference of five crackers still on the plate.
Communication
Practitioner
The student correctly uses the mathematical terms tens, number, equal.
Connections
Practitioner
The student uses two more strategies, a tens paper strip and a number bond to show that five crackers are still on the plate after subtracting the five eaten crackers. The student does not compare the two strategies to earn the Expert level.
Representation
Practitioner
The student's use of a rekenrek is appropriate to the task and accurate. The student's scribing defines the crackers eaten and the ones still on the plate. The student's place value strip is appropriate to the task and accurate. The student's scribing defines the crackers eaten and the ones still on the plate.
Overall Achievement Level:
Practitioner
Expert
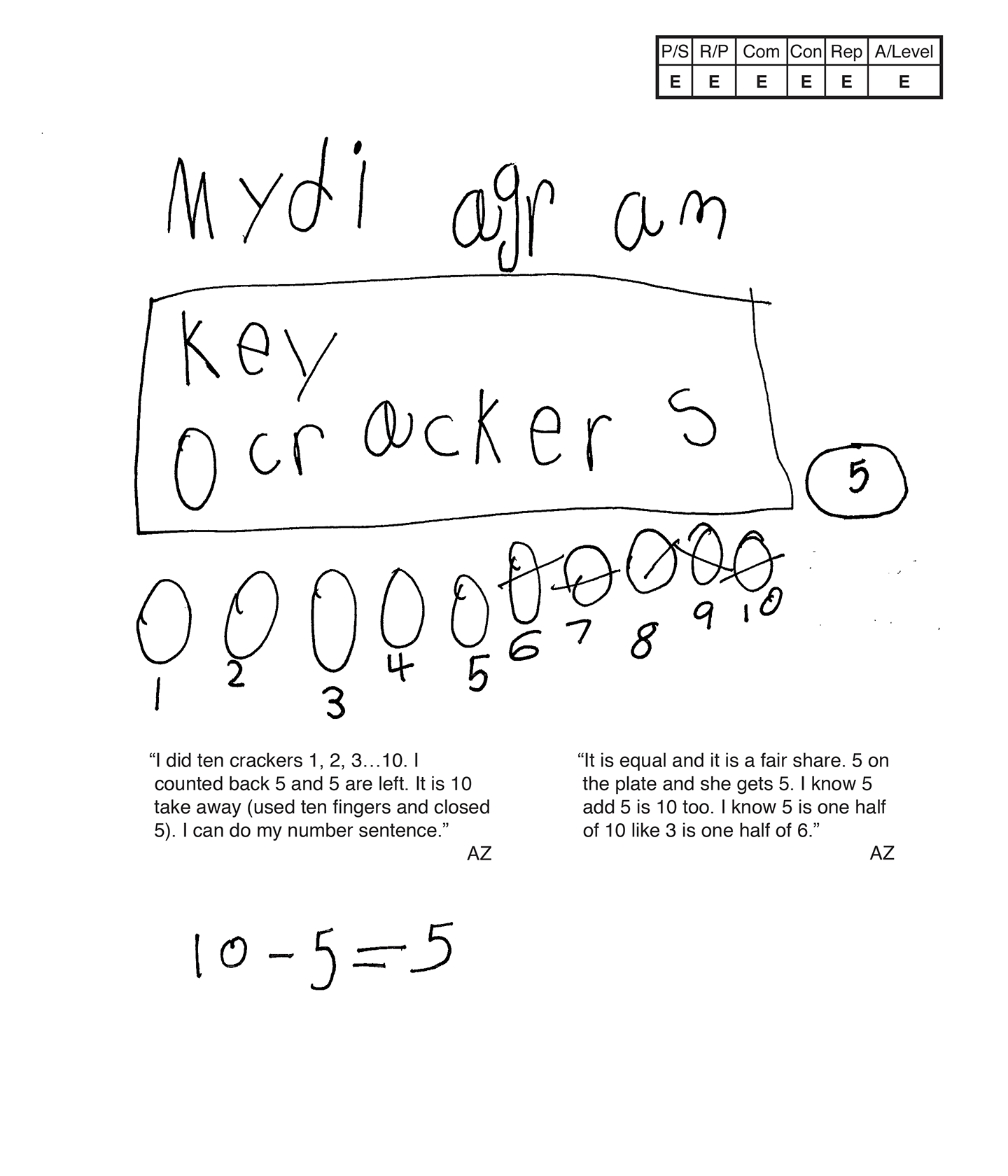 ,
, 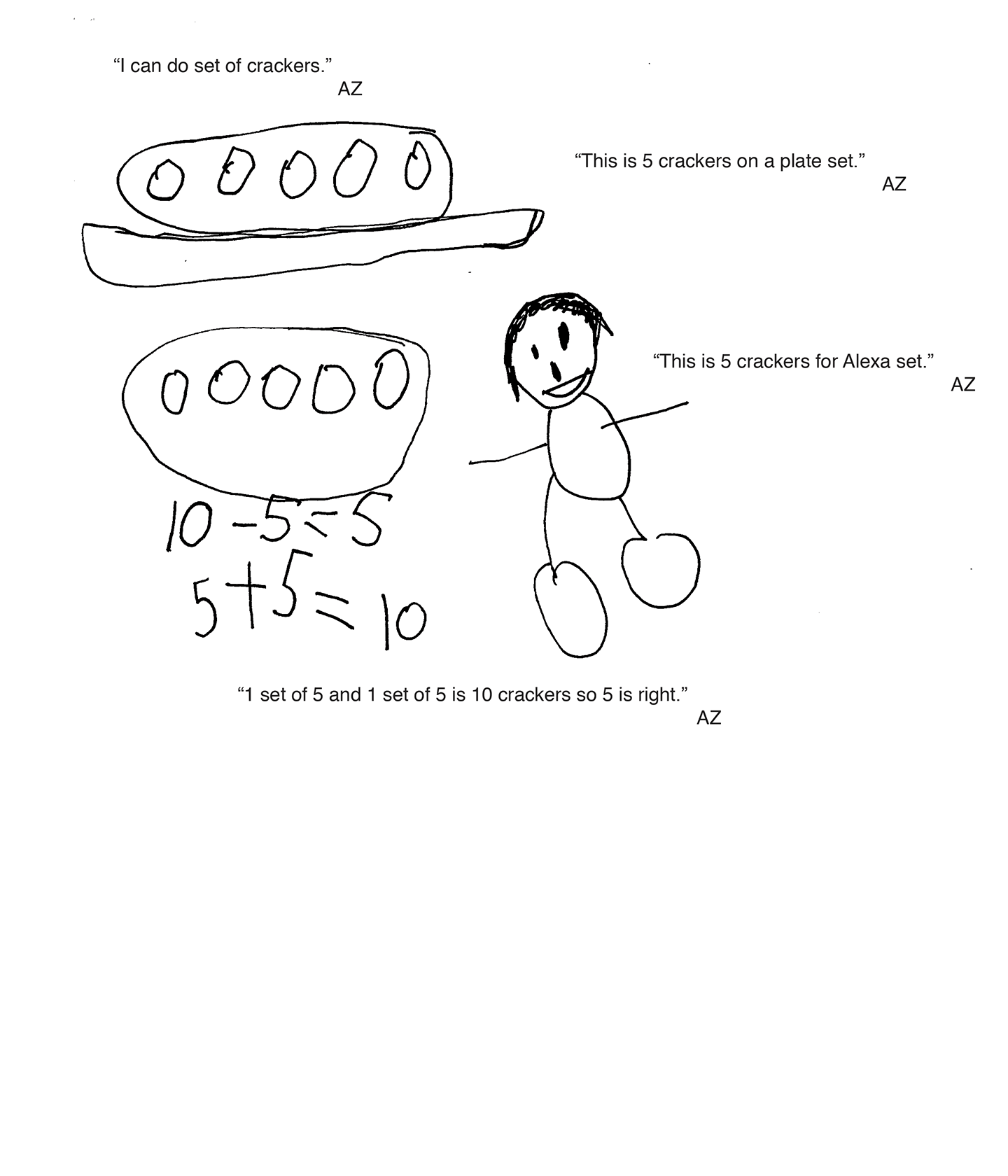
Expert 1
Scoring Rationale
Problem Solving
Expert
The student's strategy of making a diagram to show the 10 crackers, crossing out the five eaten by Alexa and also providing a subtraction equation works to solve this task. The student's answer, "5," is correct. The student uses a different strategy of diagramming sets of crackers to verify that their answer is correct.
Reasoning & Proof
Expert
The student demonstrates correct reasoning of the underlying concepts of the task. The student diagrams the correct number of crackers and subtracts out five crackers. The student also brings the understanding of fair share/equal as well as one-half. The student uses equal sets of five crackers to verify that their answer is correct.
Communication
Expert
The student correctly uses the mathematical terms diagram, key, equal, one-half, sets.
Connections
Expert
The student makes the mathematically relevant Practitioner observations, "It is equal and it is a fair share." The student makes the Expert connection of bringing the concept of one-half to their solution. The student states, "I know five is one-half of ten like three is one-half of six." The student verifies their answer by diagramming a set of five crackers on a plate and a set of five crackers that Alexa ate. The student states, "One set of five and one set of five is ten crackers so five is right."
Representation
Expert
The student's diagrams are appropriate to the task and accurate. A key defines the crackers and the scribing adds additional support to each diagram. The student creates the second diagram to verify that their answer is correct.




MP.1
Make sense of problems and persevere in solving them.