If a Bear Walks Into the Woods
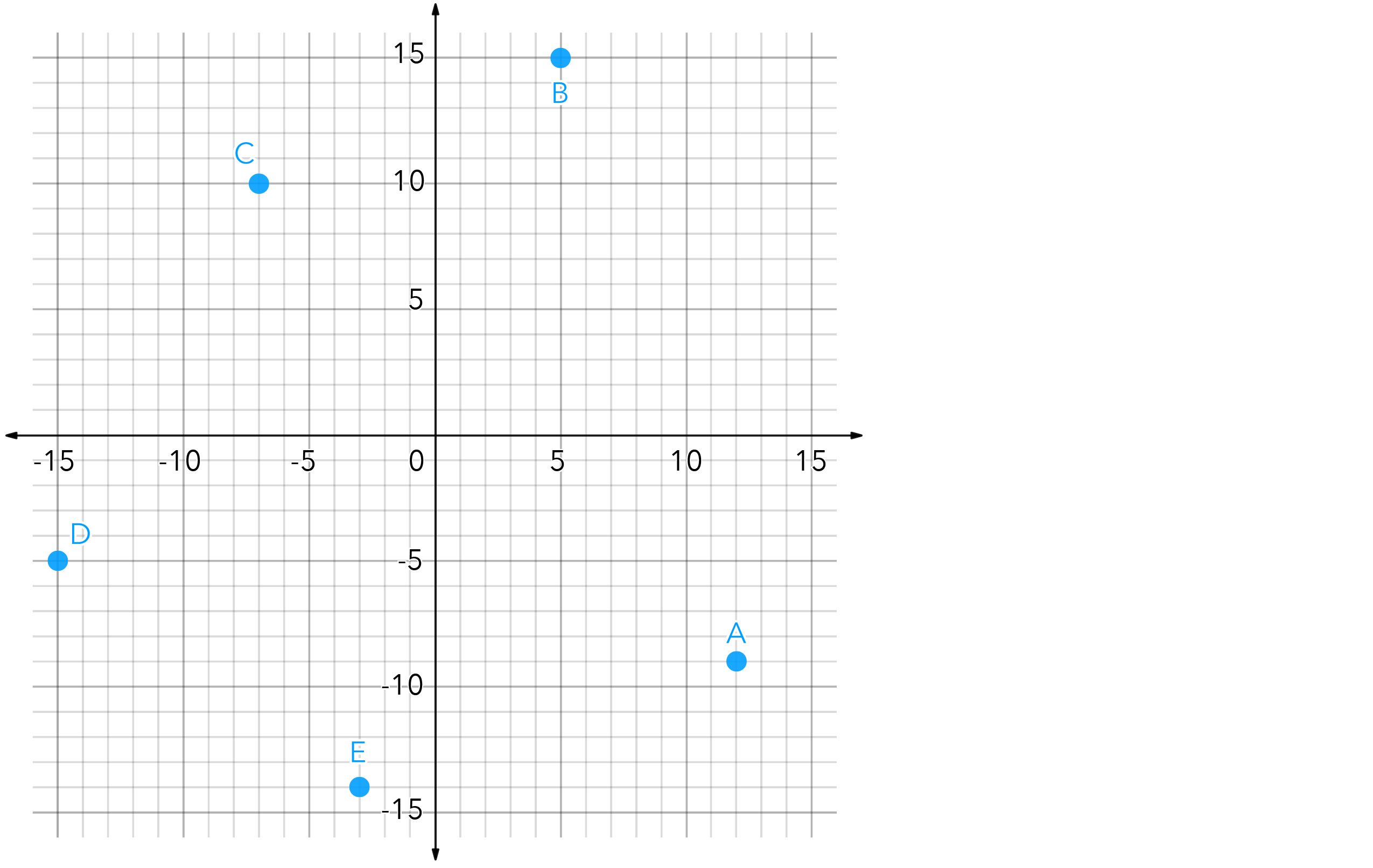
Researchers in the Denali National Park in Alaska are using GPS collars to study the habits of wild grizzly bears in the park. Granny is a mother bear who researchers have been following for over 10 years. The locations on the grid below are the specific locations where Granny spent significant time during the previous day. Researchers wanted to use the data collected to approximate how far this grizzly bear may have traveled in a given day. Granny started and ended her day at location (12, -9) and moved from location to location in alphabetical order, as indicated on the grid.
Provide researchers with a clear explanation of your calculations for how far this grizzly may have traveled.
Note: One unit on the grid represents 500 ft.
More Accessible Version
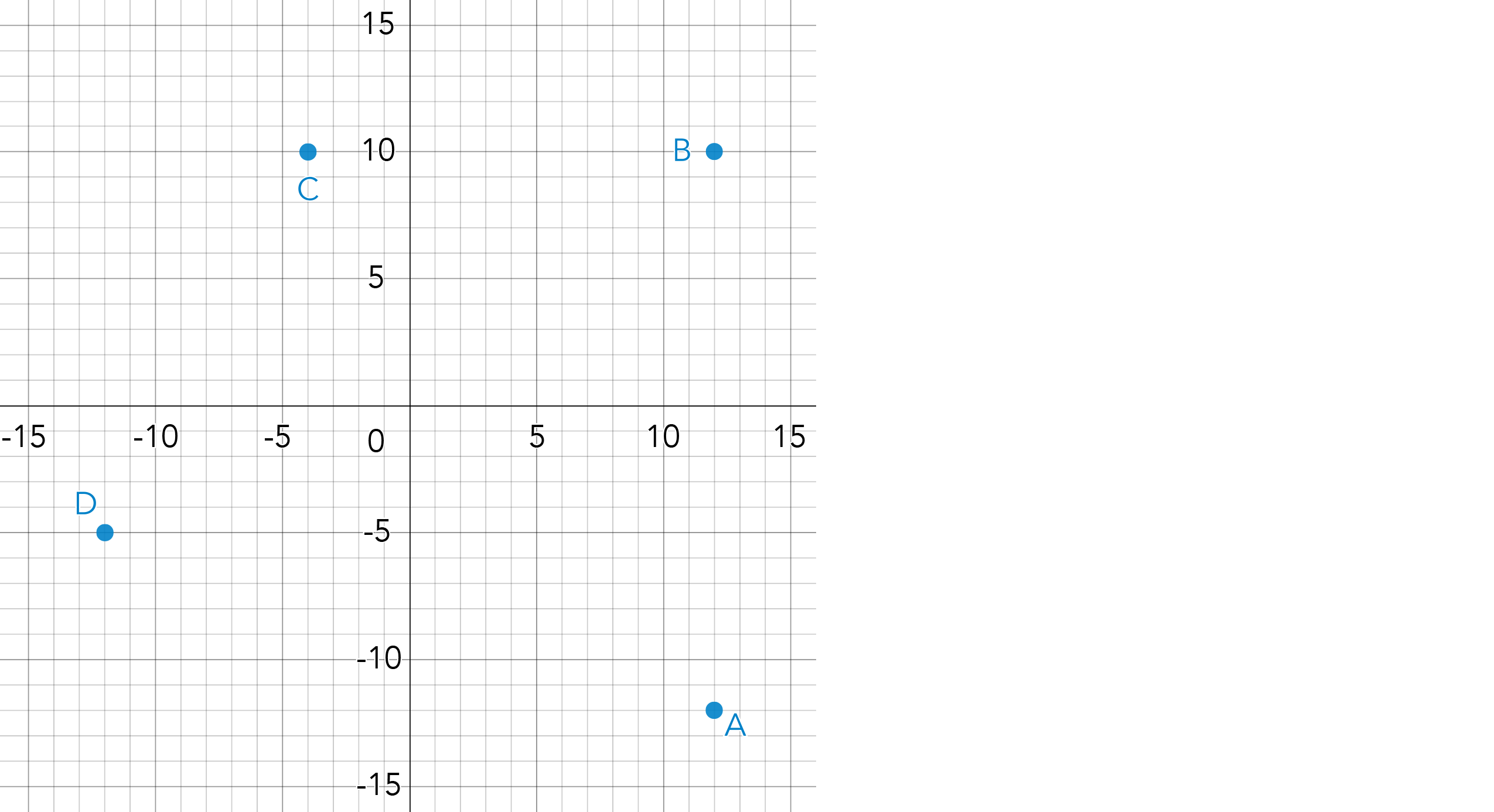
Researchers in the Denali National Park in Alaska are using GPS collars to study the habits of wild grizzly bears in the park. Granny is a mother bear who researchers have been following for over 10 years. The locations on the grid below are the specific locations where Granny spent significant time during the previous day. Researchers wanted to use the data collected to approximate how far this grizzly bear may have traveled in a given day. Granny started and ended her day at location (12, -12) and moved from location to location in alphabetical order, as indicated on the grid.
Provide researchers with a clear explanation of your calculations for how far this grizzly may have traveled.
Note: One unit on the grid represents 100 meters.
More Challenging Version
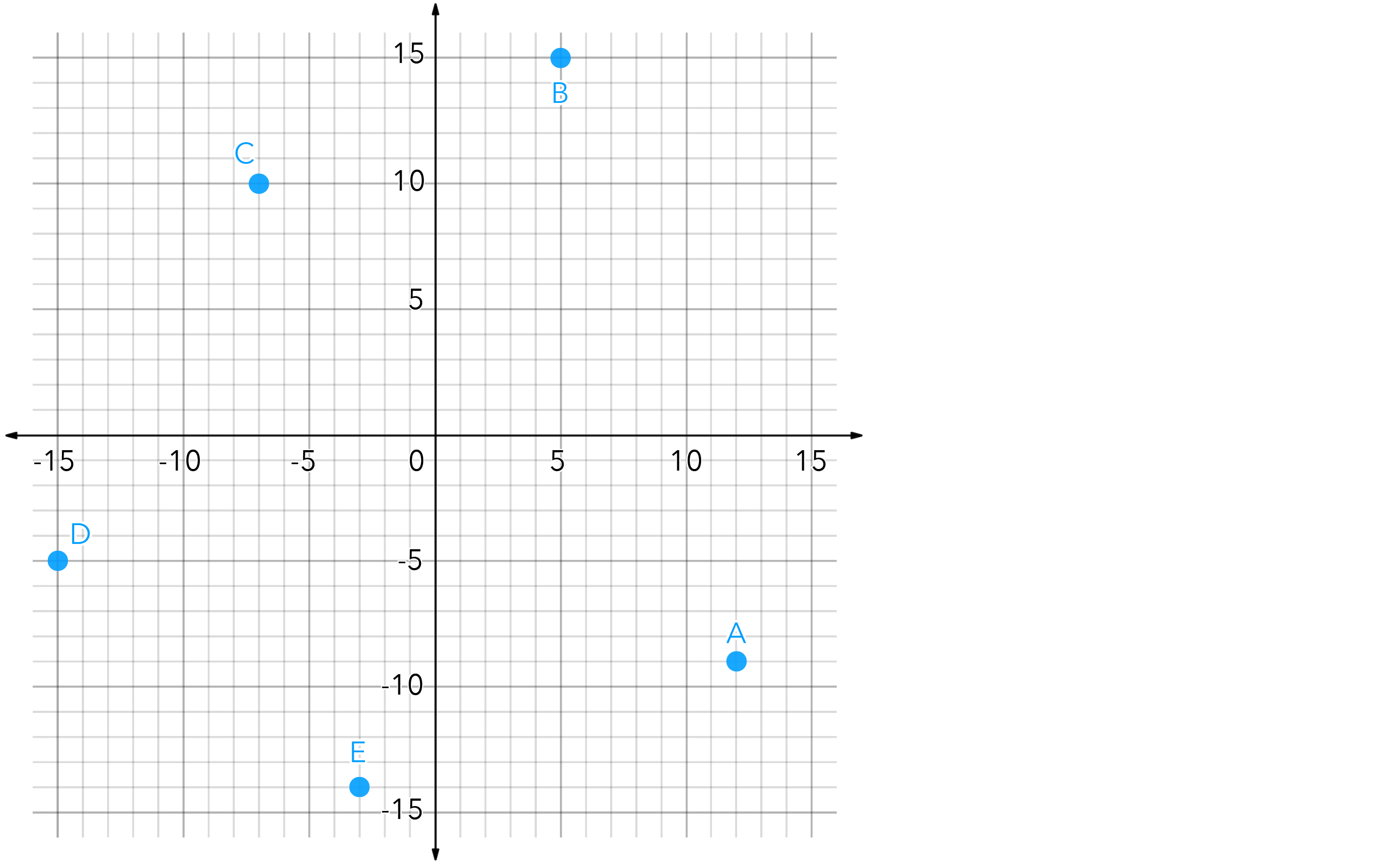
Researchers in the Denali National Park in Alaska are using GPS collars to study the habits of wild grizzly bears in the park. Granny is a mother bear who researchers have been following for over 10 years. The locations on the grid below are the specific locations where Granny spent significant time during the previous day. Researchers wanted to use the data collected to approximate how far this grizzly bear may have traveled in a given day. Researchers are also trying to determine the total area of the territory Granny seems to utilize.
Granny started and ended her day at location (12, -9) and moved from location to location in alphabetical order, as indicated on the grid.
Provide researchers with a clear explanation of your calculations for how far this grizzly may have traveled and the area of her territory.
Note: One unit on the grid represents 500 ft.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
Teacher Notes:
Possible questions to pose during the launch of this task:
- How can you draw a right triangle between each pair of points?
- Why can grid lines be used to find the lengths of the legs of the triangle but not the hypotenuse?
- Between each pair of points, what’s a distance that’s too high, what’s a distance that’s too low?
Possible misconceptions that students may encounter:
- Students may forget to convert the units on the grid to feet.
- Students may try to count the squares between each point and use this as the distance.
- Students may think the sum of the 2 legs is equal to the length of the hypotenuse.
- Students might think that the sum of the squares of the 2 legs is equal to the hypotenuse.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.



MP.2
Reason abstractly and quantitatively.