Sharing Muffins
Nine friends are going to equally share some muffins. Each muffin is the same size. Each friend gets one and one-third muffins. How many muffins did the nine friends equally share? Show all your mathematical thinking.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
A student may independently select a printed number line, number chart, ten frames, graph paper, etc. as they work on a task.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.
Possible Solutions
Assess
Novice

Novice 1
Scoring Rationale
Problem Solving
Novice
The student's strategy of using a diagram to show eight friends with 1/3 written under each friend and adding the 1/3s for a total of 8/24 would not work to solve the task. The student's answer, "8 muffins," is not correct.
Reasoning & Proof
Novice
The student does not indicate nine friends. The student does not show correct understanding of adding 1 1/3 nine times. The student adds the numerator and denominator of 1/3 eight times and uses the numerator total of eight as their answer.
Communication
Novice
The student does not use any mathematical language. The student does not earn credit for the mathematical notation 1/3, 8/24 because the student does not demonstrate correct fractional understanding.
Connections
Novice
The student solves the task and stops without making a mathematically relevant connection.
Representation
Apprentice
The student attempts a diagram of friends and notes 1/3 for each friend. This is not accurate. The student provides no labels for the friends or the 1/3 notation.
Overall Achievement Level:
Novice
Apprentice
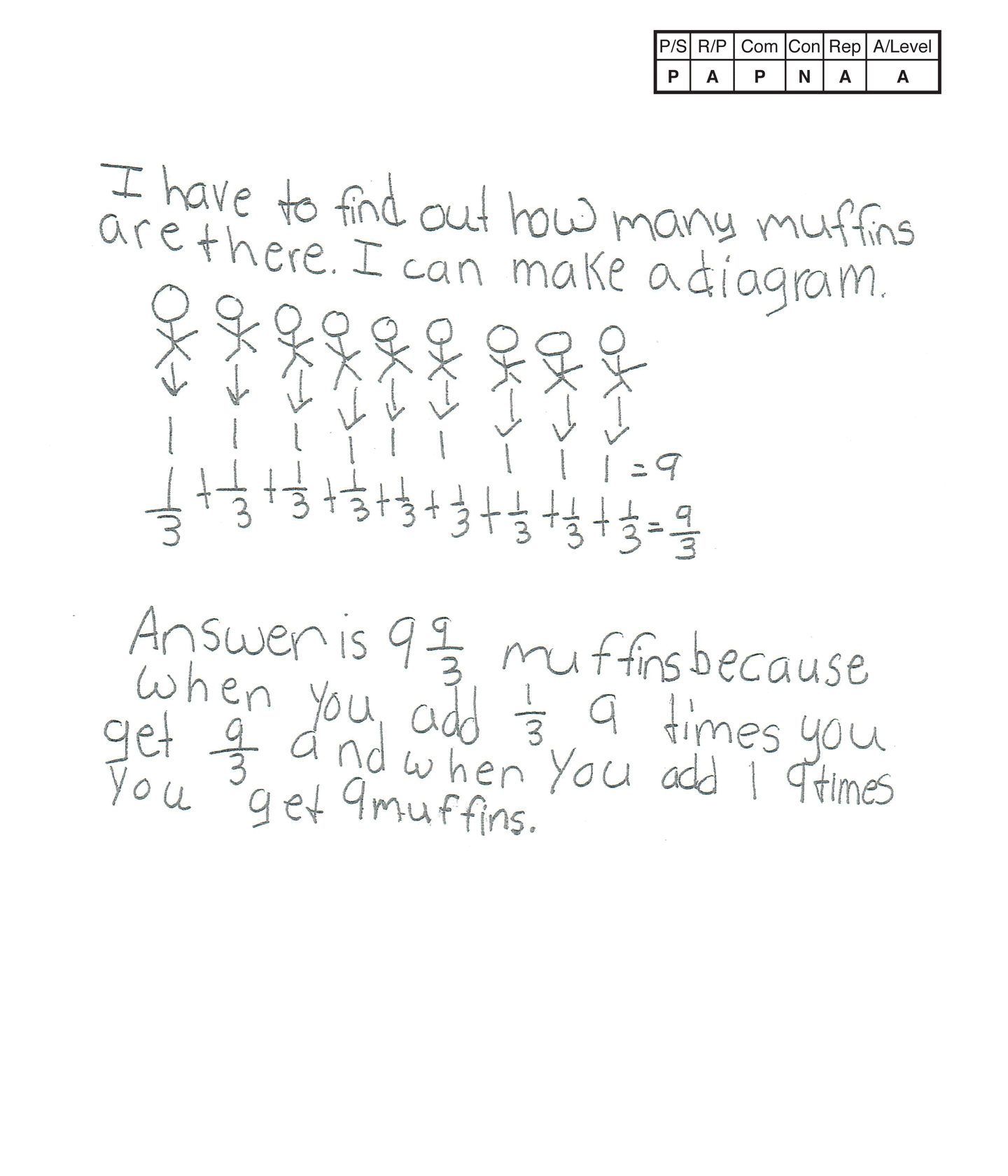
Apprentice 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a diagram to show nine friends with 1 1/3 muffins each and a total of 9 9/3 muffins works to solve the task. The student's answer, "Answer is 9 9/3 muffins because when you add 1/3 9 times you get 9/3 and when you add 1 9 times you get 9 muffins," is correct.
Reasoning & Proof
Apprentice
The student demonstrates correct understanding of whole and fractional parts of a whole to arrive at an answer of 9 9/3 muffins. In this real-world problem-solving situation it would be expected to simplify the mixed number for a total of 12 muffins. The student does not demonstrate this correct reasoning.
Communication
Practitioner
The student correctly uses the mathematical term diagram. The student correctly uses the mathematical notation 1/3, 9 9/3, 9/3.
Connections
Novice
The student solves the task and stops without making a mathematically relevant connection.
Representation
Apprentice
The student's diagram is appropriate but not accurate. The student does not provide a key or text to label the nine friends. The student's answer provides the muffin label.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for “Using the Assessment Rubric.”
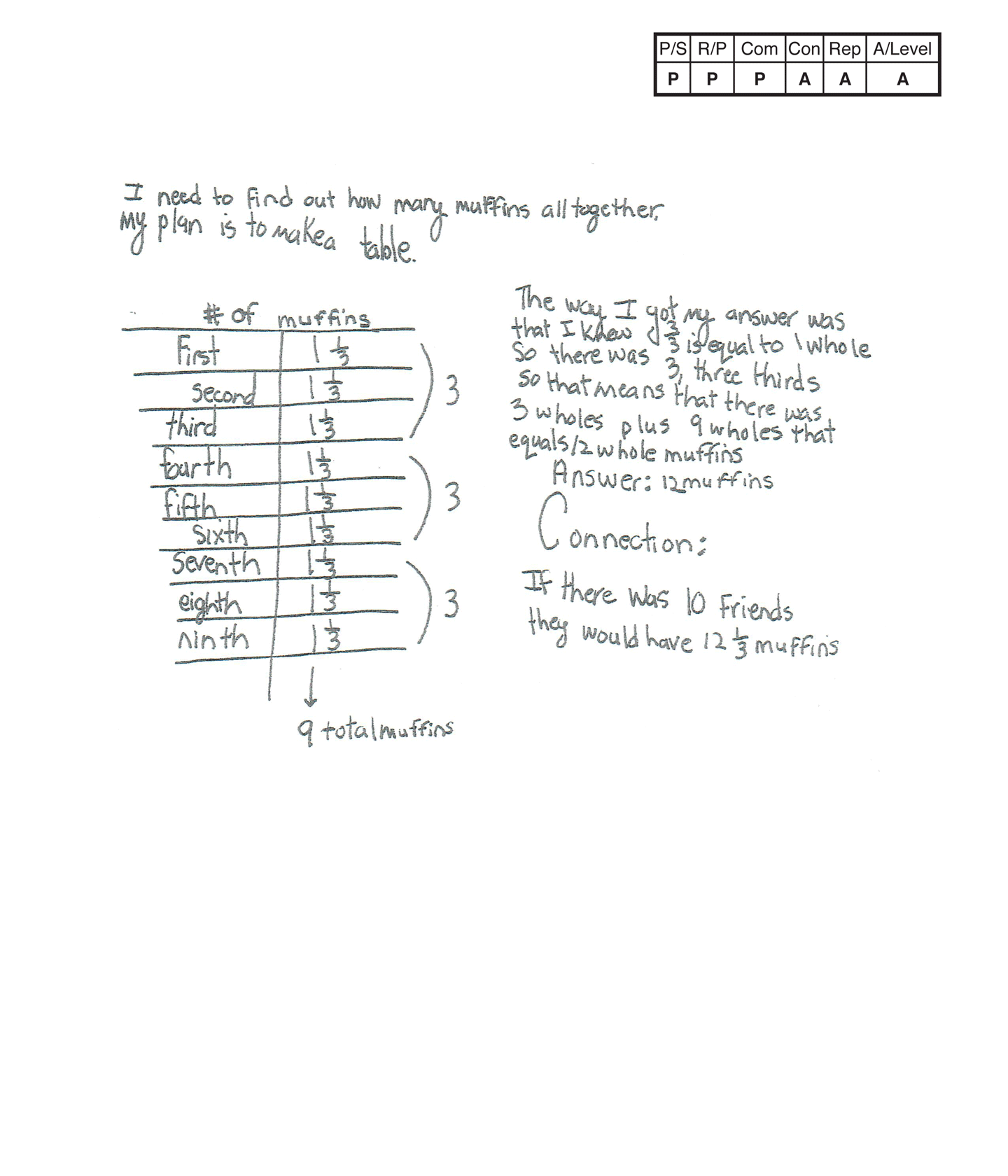
Apprentice 2
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a table to show nine friends with 1 1/3 muffins each for a total of 12 muffins works to solve the task. The student's answer, "12 muffins," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct understanding of the underlying mathematical concepts of whole, fractional parts of a whole, and addition of fractions.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, equal, whole, three-thirds, total. The student correctly uses the mathematical notation 1 1/3, 3/3.
Connections
Apprentice
The student attempts a connection by adding another friend. The total muffins for 10 friends would be 13 1/3 muffins and not 12 1/3 muffins. A connection has to be accurate to earn the Practitioner level.
Representation
Apprentice
The student's diagram is appropriate but not accurate. It appears that "# of muffins" is the title of the table. The column labels of friends and muffins are missing.
Overall Achievement Level:
Apprentice
Practitioner
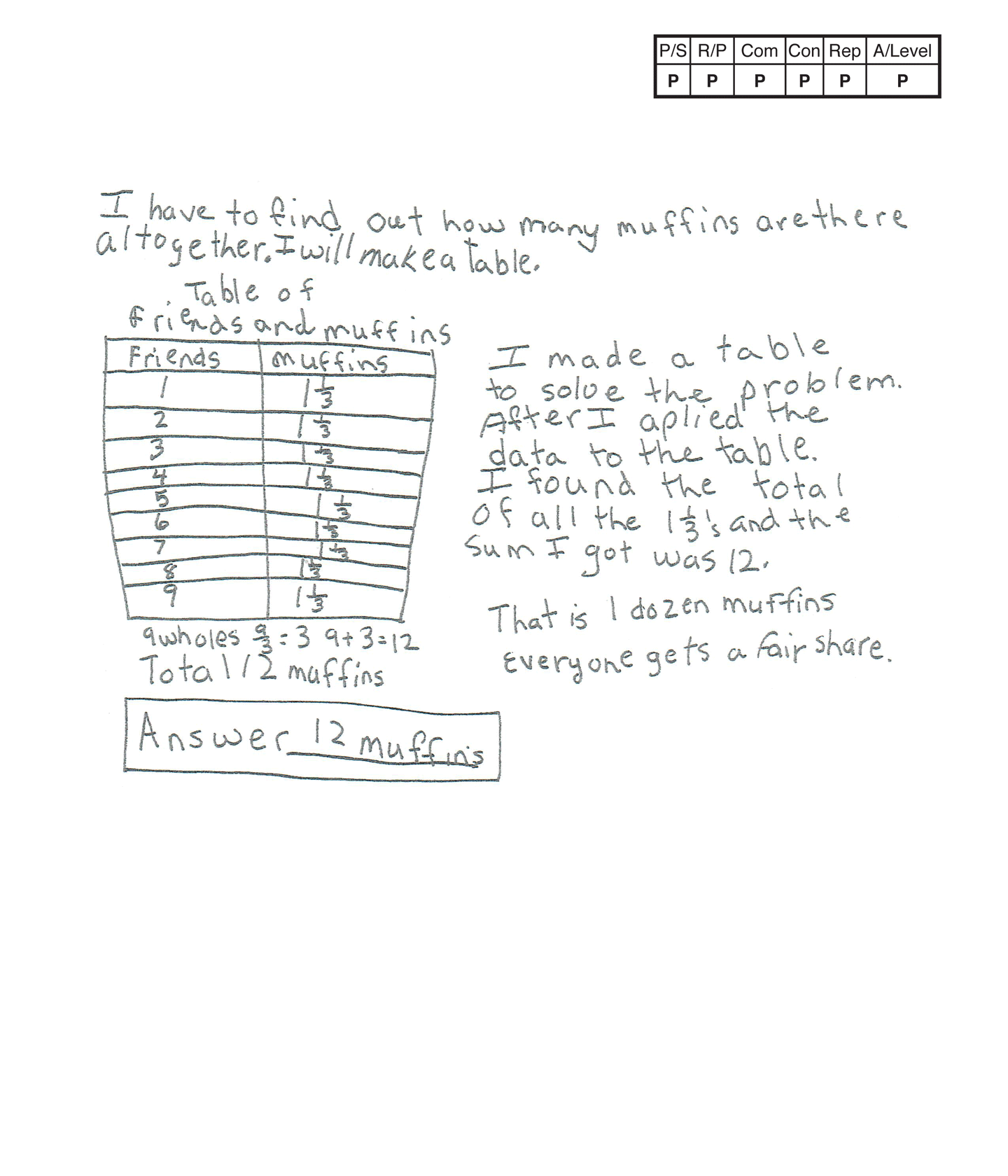
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a table to show nine friends with 1 1/3 muffins each for a total of 12 muffins works to solve the task. The student's answer, "12 muffins," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct understanding of the underlying mathematical concepts of whole, fractional parts of a whole, and addition of fractions.
Communication
Practitioner
The student correctly uses the mathematical terms table, data, total, sum, dozen, fair share. The student correctly uses the mathematical notation 1 1/3, 9/3.
Connections
Practitioner
The student makes the mathematically relevant observations, "That is 1 dozen muffins," and, "Everyone gets a fair share."
Representation
Practitioner
The student's table is appropriate and accurate. The student provides a title, each column is correctly labeled and the entered data is correct.
Overall Achievement Level:
Practitioner
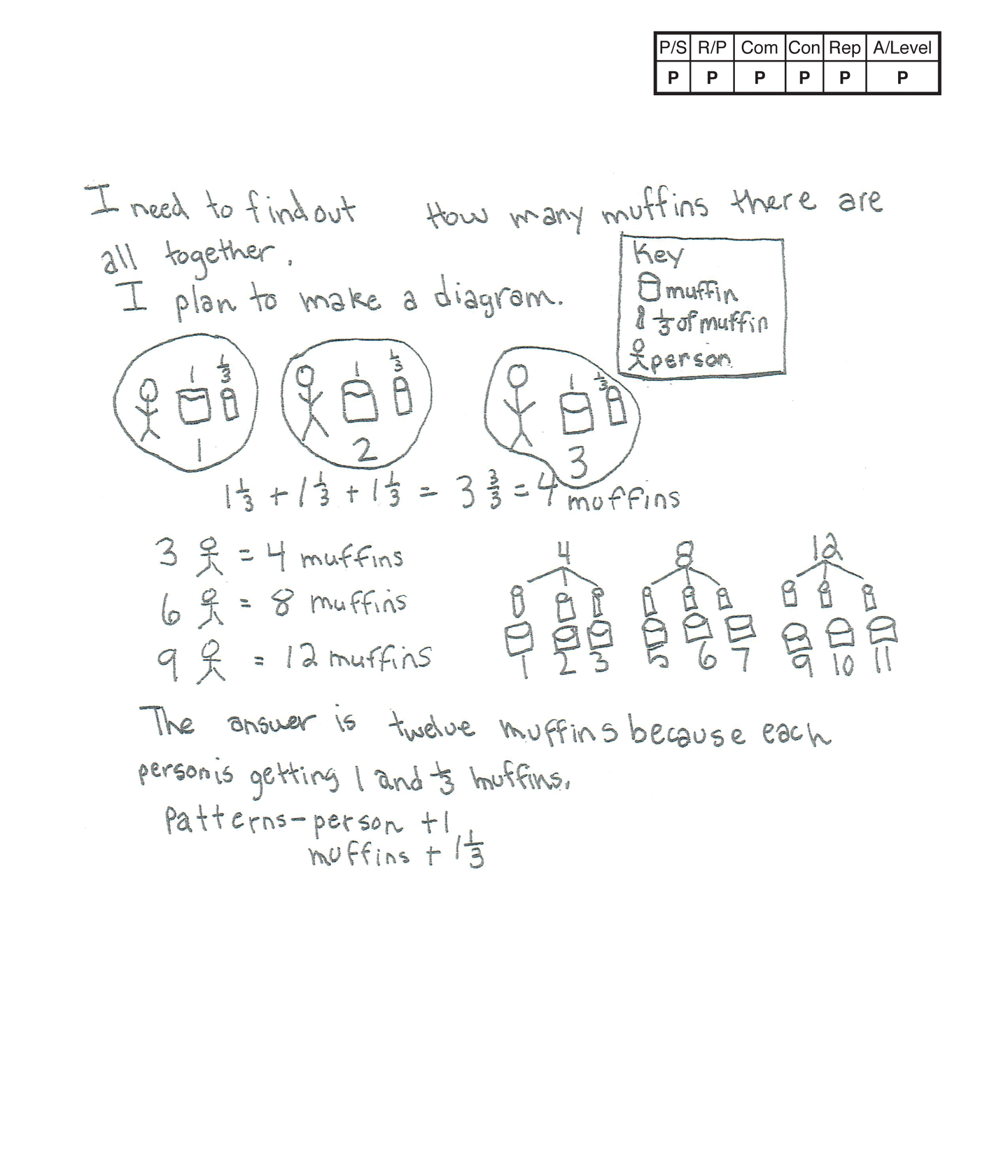
Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a diagram to show a group of three friends with 1 1/3 muffins each for a total of four muffins and then adding two more groups of three friends for a total of 12 muffins works to solve the task. The student also includes a second diagram to show counting on from the first diagram for four, eight, and 12 muffins. The student's answer, "The answer is twelve muffins because each person is getting 1 and 1/3 muffins," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct understanding of the underlying mathematical concepts of whole, fractional parts of a whole, addition of fractions, and totaling groups of muffins. The student uses one diagram to demonstrate how the first four muffins were determined and then a second diagram to continue a running total of four, eight, and 12 muffins.
Communication
Practitioner
The student correctly uses the mathematical terms diagram, key, patterns. The student correctly uses the mathematical notation 1/3, 1 1/3, 3 3/3.
Connections
Practitioner
The student makes the mathematically relevant observation, "Patterns—person +1, muffins +1 1/3."
Representation
Practitioner
The student's two diagrams are appropriate and accurate. The student provides a key to define a muffin, 1/3 of a muffin and a person.
Overall Achievement Level:
Practitioner
 ,
, 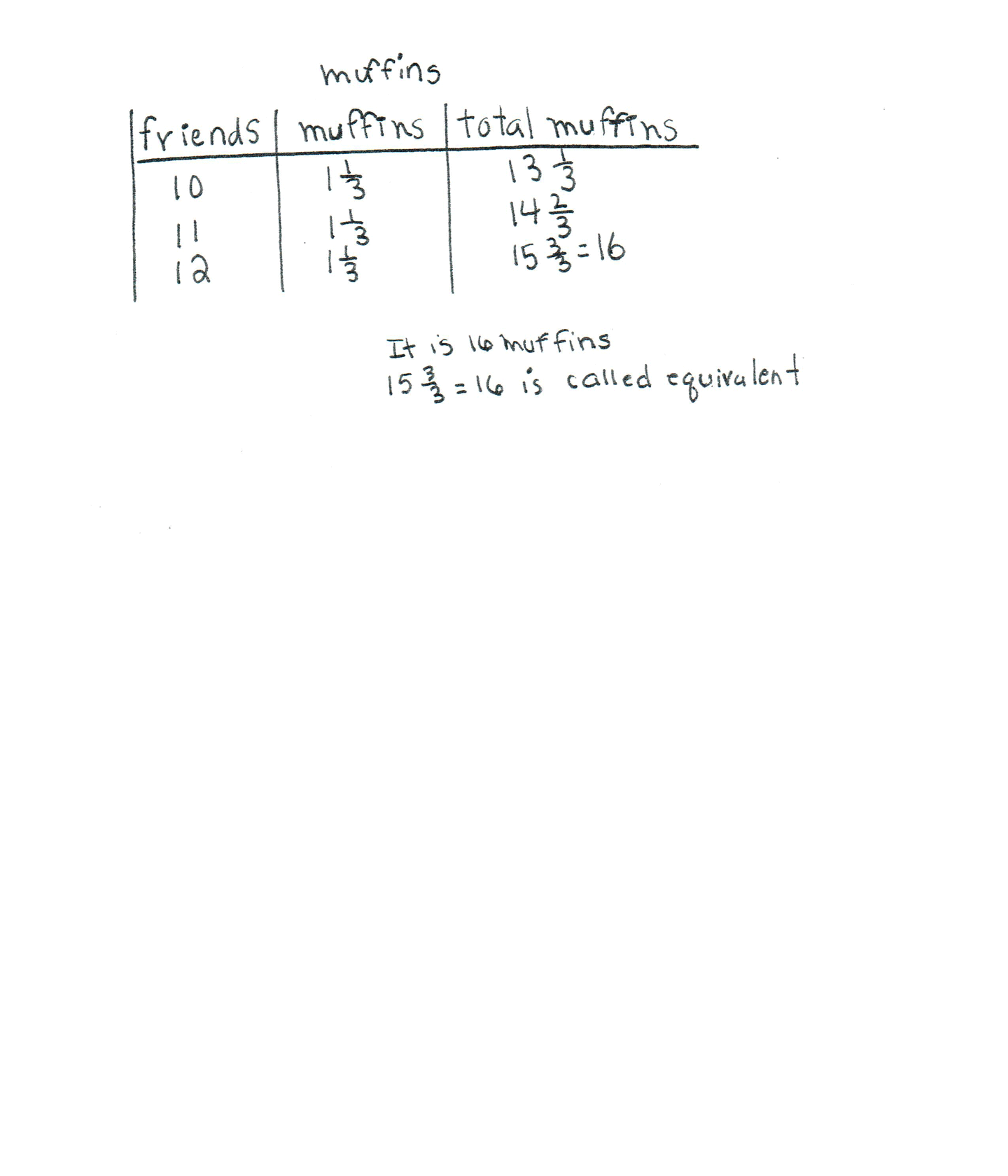
Practitioner 3
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of using a table to show the friends, muffins, total of 12 muffins, and total mixed numbers of muffins, works to solve the task. The student's answer, "12 muffins," is correct.
Reasoning & Proof
Practitioner
The student demonstrates correct understanding of the underlying mathematical concepts of whole, fractional parts of a whole, and addition of fractions to find a total amount of muffins.
Communication
Practitioner
The student correctly uses the mathematical terms table, total, key, equals, dozen, whole number, equivalent. The student correctly uses the mathematical notation 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th, 9th, 1 1/3, 2 2/3, 3 3/3, 5 1/3, 6 2/3, 7 3/3, 9 1/3, 10 2/3, 11 3/3, 4/3, 9/3, 16/3, 20/3, 24/3, 28/3, 32/3, 36/3, 13 1/3, 14 2/3, 15 3/3.
Connections
Practitioner
The student makes the mathematically relevant observations, "12 is a dozen," and, "15 3/3 = 16 is called equivalent." The student recreates the task to continue to the next whole number of muffins and discovers that it is sixteen muffins. The student states, "I will keep going the next whole number of muffins." and, "It is 16 muffins."
Representation
Practitioner
The student's first table is appropriate but not accurate. The third row for total improper fractions should read 12/3 and not 9/3. The student's second table is appropriate and accurate. Both tables have an accurate title and the labels for each column are correct. Only one representation out of two, three, etc. needs to be appropriate and accurate to be assessed the Practitioner Level.
Overall Achievement Level:
Practitioner
Expert
 ,
, 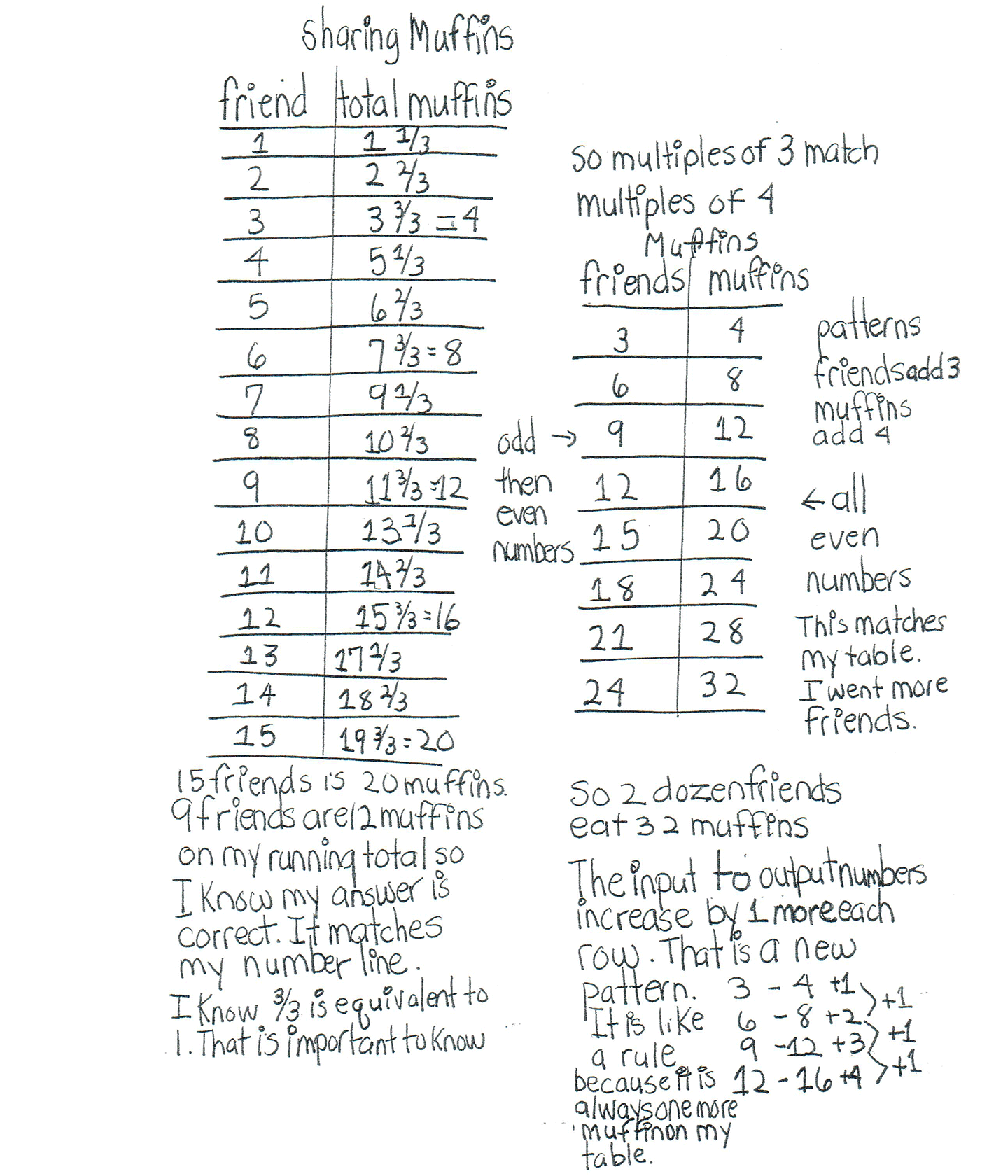 ,
, 
Expert 1
Scoring Rationale
Problem Solving
Expert
The student's strategy of using a number line to show the number of muffins per friend and the total number of muffins works to solve the task. The student's answer, "The answer is twelve muffins," is correct. The student uses an alternative strategy of a table to verify their answer, and brings the knowledge of percents to the task.
Reasoning & Proof
Expert
The student demonstrates correct understanding of the underlying mathematical concepts of whole, fractional parts of a whole, and addition of fractions to find a total amount of muffins. The student verifies that their answer is correct by using a table. The student makes a generalization about the multiples of three and four determining whole numbers of muffins and shows understanding of 33 1/3%.
Communication
Expert
The student correctly uses the mathematical terms total, amount, number line, per, patterns, dozen, table, whole, multiples, odd, even numbers, running total, equivalent, dozen, input, output, row, rule, more, percents, diagrams. The student correctly uses the mathematical notation 1 1/3, 13 1/3, 14 2/3, 8/3, 32/3, 2 2/3, 3 3/3, 5 1/3, 6 2/3, 7 3/3, 9 1/3, 10 2/3, 11 3/3, 15 3/3, 17 1/3, 18 2/3, 19 3/3, 3/3, 100%, 33 1/3%, 1 1/2, 13 1/2.
Connections
Expert
The student makes the mathematically relevant Practitioner observations, "Patterns friend add 1, muffins add 1 1/3," "They ate a dozen muffins," "I can do some improper fractions. 2 friends is 8/3, 8 friends is 32/3," "You shouldn't leave them that way. You want to say 2 2/3 and 10 2/3 muffins. no one buys parts of muffins so you got to see whole muffins," "odd then even numbers," "patterns friends add 3, muffins add 4," "all even numbers," "I know 3/3 is equivalent to 1. That is important to know," "So 2 dozen friends eat 32 muffins," and, "If each friend eats 1 1/2 muffin you need 13 1/2 muffins so you have to buy 14 muffins." The student makes Expert connections. The student lists the number of muffins for 10, 11, and 12 friends and predicts, "so I think 15 friends is 20 muffins." The student verifies their thinking. "I can make a table to prove this and my answer." The student makes a table of 15 friends and muffins and states, "15 friends is 20 muffins. 9 friends are 12 muffins on my running total so I know my answer is correct. It matches my number line." The student makes another table to support their thinking that "the multiples of 3 match multiples of 4." The student states, "This matches my table. I went more friends." The student makes a generalization about their table of multiples. "The input to output numbers increase by 1 more each row That is a new pattern. It is like a rule because it is always one more muffin on my table. 3 - 4 + 1, 6 - 8 + 2, 9 - 12 + 3, 12 - 16 + 4" (with the + 1 pattern also indicated). The student also uses a diagram to compare a whole muffin to 100% and 1/3 of a muffin to 33 1/3%.
Representation
Expert
The student's number line is appropriate to the problem and accurate. All necessary labels are indicated and the spacing between fractional parts is correct. The student's two tables are appropriate and accurate. All titles and column labels are correct and all entered data is correct. The student's diagram is appropriate and accurate. The muffins and fractional parts of one muffin are labeled correctly. The student uses their representations to verify the answer and support generalizations formed from patterns found in their tables.



MP.1
Make sense of problems and persevere in solving them.