Scary Reunion
A team of marine biologists are studying sharks in the Caribbean. The team has anchored their research vessel near the island of South Caicos. At 9 a.m., the team tagged two sharks with radio transmitters and released them. At 2 p.m., the team noted the location of the two sharks.
New locations:
Shark 1: Located 45 miles north and 60 miles west.
Shark 2: Located 36 miles south and 77 miles east.
If the team wanted to pull up the anchor at 2 p.m. and be in the same location as one of the sharks by 7 p.m., how fast would the research vessel need to travel to be in a location near one of the sharks? Assume each shark maintains its current speed and direction.
Provide a clear explanation of your calculations for the team.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
Teacher Notes:
Possible questions to pose during the launch of this task:
- What does the path of the sharks and vessel look like?
- How do you find speed?
Possible misconceptions that students may encounter:
- Students may try to use the distance to the shark at 2 pm and not take into account that the sharks are still traveling further.
- Students may misinterpret the locations given as the path each shark takes.
- Even though the sharks may not move in a straight path this won’t impact the distance and speed the vessel needs to travel. Acting out what happens can help students recognize this.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task in the classroom, to prepare students, to promote discussion, and to inspire engagement and problem solving.
Possible Solutions
Assess
Novice

Novice 1
Scoring Rationale
Problem Solving
Apprentice
The student’s strategy of constructing a graph to show the location of each shark would work but the student does not correctly plot the points nor calculate the actual distance traveled. The students answers of “a team of marine biologists will need to travel 45 miles per hour to be in the same location of shark 1” and “the marine biologists will need to travel 51 miles per hour to see shark 2” are incorrect.
Reasoning & Proof
Novice
The student does not demonstrate understanding of the underlying concepts of finding the distance traveled using a coordinate plane or the Pythagorean Theorem. There is no justification for reasoning present and arguments are made with no mathematical basis.
Communication
Apprentice
The appropriate use of formal math language is minimal with miles per hour and graph. The student makes no attempt to provide a written account of their approach for finding 45 miles per hour or 51 miles per hour.
Connections
Novice
The student does not make a mathematical connection about their solution.
Representation
Apprentice
The student attempts to make a coordinate graph but does not accurately plot the location of shark 1, does not include labels, does not use it to find the distance or speed traveled.
Overall Achievement Level:
Novice
Apprentice
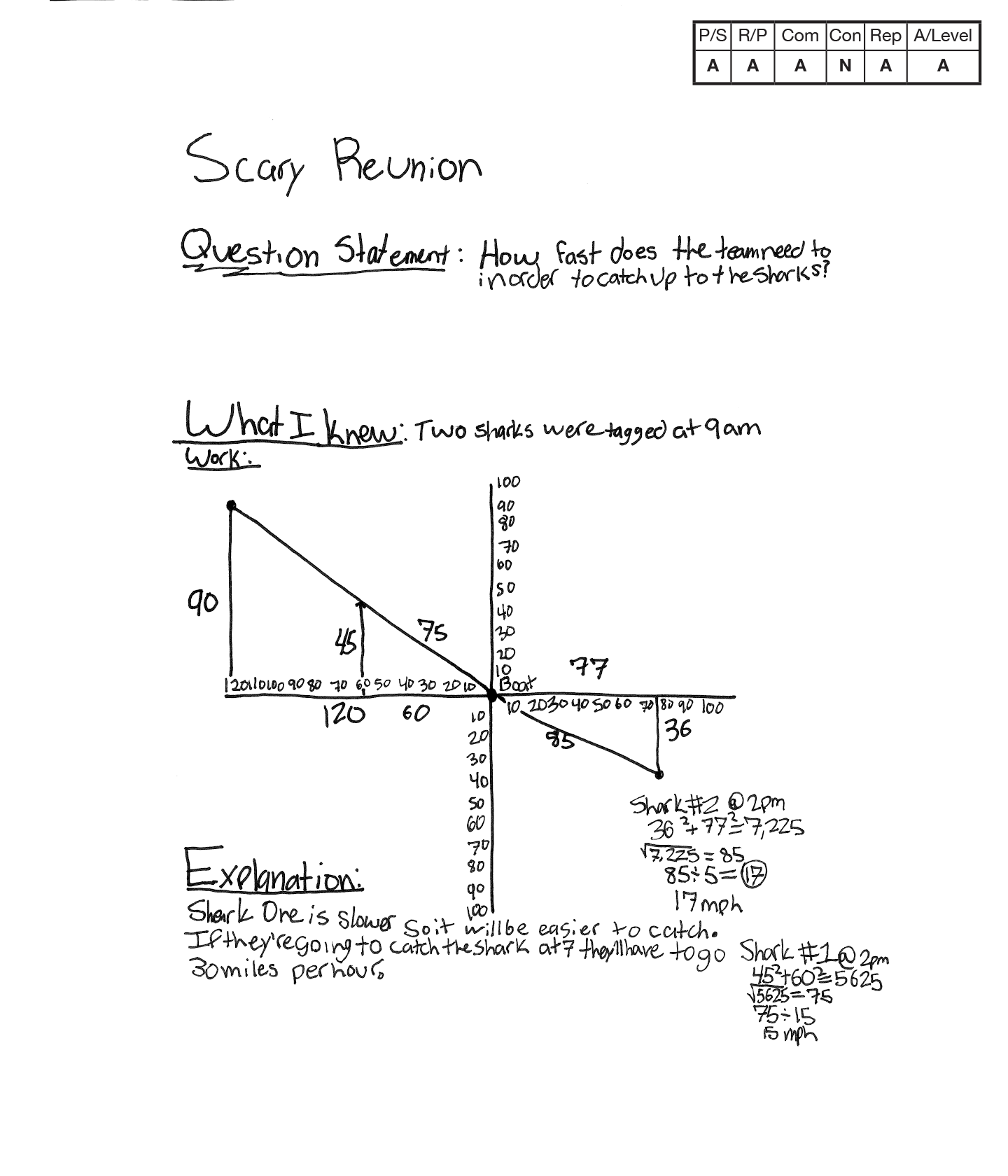
Apprentice 1
Scoring Rationale
Problem Solving
Apprentice
The student’s strategy of using the Pythagorean Theorem works to solve the first part of the task. The student’s answer for the first part of the task is correct, “Shark #2 @ 2 pm = 17 mph” and “Shark #1 @ 2 pm = 15 mph.” The student provides no evidence of their strategy that therefore converting the Shark #1 speed of 15 mph to the boat needing to go 30 mph.
Reasoning & Proof
Apprentice
The student demonstrates correct reasoning for some of the underlying concepts of the task, such as using the Pythagorean Theorem to calculate the distance traveled by each shark at 2 pm, “362 + 772 = 7225, `sqrt 7225` = 85” and “452 + 602 = 5625, `sqrt 5625` = 75.” The student does not show correct reasoning for calculating the speed of shark or vessel. The student does not provide mathematical justification for “85`-:` 5 = 17 mph”, “75`-:` 5 = 15 mph”, and “they’ll have to go 30 miles per hour.”
Communication
Apprentice
The student attempts to make an organized and sequenced response, but it is incomplete. The does not communicate their approach including the use of the Pythagorean Theorem, the formula for speed, or why the boat will have to go 30 mph. The appropriate use of formal math language is minimal including fast, mph, slower, miles per hour.
Connections
Novice
The student’s connection is contextually irrelevant, “Shark One is slower so it will be easier to catch” as it does not explore the concept of the formula for speed.
Representation
Apprentice
The student attempts to construct a coordinate grid to investigate the location of the shark after 5 hours. The student does not provide any labels for the data provided on the grid or for the units on the x and y coordinates.
Overall Achievement Level:
Apprentice
The overall achievement level for this piece of student work falls under Exemplars exception to the rule category. If a student has all Apprentice scores or above, but a Novice in "Connections," the student may still receive an achievement level score of Apprentice. To learn more about Exemplars scoring, please refer to the section of your dashboard called "Tools for Success" and click on the link for “Using the Assessment Rubric.”

Apprentice 2
Scoring Rationale
Problem Solving
Apprentice
The student makes mistakes in determining how far the sharks traveled. The student correctly uses the Pythagorean Theorem for incorrect values of the distances traveled by each shark. The student correctly uses the formula for speed but arrives at an incorrect answer due to their previous mistake. The student incorrectly states “The boat would have to go 17.1 or 17 mph to be near shark 1 at 7 pm” and “The boat would have to go 19.3 or 19 mph to be near shark 2 at 7 pm.”
Reasoning & Proof
Practitioner
The student demonstrates correct reasoning of the Pythagorean Theorem, “452 + 1652 = c2” and “362 + 1902 = c2”. The student correctly uses the formula for speed, “speed = distance`-:` time” to provide mathematical justification for the speed of the sharks, “171`-:` 10 = 17.1 mph”, and “193`-:` 10 = 19.3 mph.”
Communication
Apprentice
The student attempts to construct an organized, sequenced and labeled response but is inconsistent on defining each step of their approach. The student does not explain why they used “60 + 45 = 105” and “36 + 77 = 113” to determine how far each shark traveled in the first five hours.
Connections
Apprentice
The student attempts to make a mathematically relevant connection, “I realized that I need to find the hypotenuse first.” This connection is relevant but does not explore or clarify how this would change their approach or final answer.
Representation
Practitioner
The student constructs multiple diagrams to help them solve the problem and to portray their thinking. The diagrams appropriately and accurately represent the student’s approach that illustrates where mathematical misconceptions occurred.
Overall Achievement Level:
Apprentice
Practitioner
 ,
, 
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
The student’s strategy of plotting the position of each shark on a coordinate grid and using the Pythagorean Theorem to calculate the distance traveled in the first 5 hours works to solve the task. The student's answer of the boat needing to travel 30 mph to catch shark 1 and 34 mph to catch shark 2 is correct.
Reasoning & Proof
Practitioner
The student shows understanding that the Pythagorean Theorem can be used to calculate the distance each shark traveled, “452 + 602 = 5,625 = c2, c = 75 miles.” The student correctly calculates the speed of each shark, “75 ÷ 5 = 15 mph” and “85 ÷ 5 hrs = 17 mph” and then determines the speed of the boat “which is double the distance at 2 pm.”
Communication
Practitioner
The student correctly identifies the problem to be solved in their opening statement, describes their approach in an organized and coherent response, and states a correct conclusion. Appropriate formal math language such as Pythagorean Theorem, mph, distance, graph, double, constant rate is used to share and clarify ideas.
Connections
Practitioner
The student makes a mathematically relevant connection by exploring the concept of a ”constant rate of 15 mph”. The student uses this connection to determine to double the speed of the boat to catch the shark in 5 hours.
Representation
Expert
The student’s coordinate grid is appropriate and accurate for determining the location of the shark after 5 hours and after 10 hours. The student uses the coordinate grid to analyze the relationship between the distance traveled in the first 5 hours and in the second five hours. All necessary labels are provided and the entered data is correct.
Overall Achievement Level:
Practitioner

Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
The student’s strategy of drawing diagrams to show the shark’s journey, using the Pythagorean Theorem to calculate the sharks’ distance traveled in 5 hours, and the formula for speed effectively solves the task. The student's answer of needing to travel 30 mph to be near shark 1 and to go 34 mph to be near shark 2 is correct.
Reasoning & Proof
Practitioner
The student correctly applies the Pythagorean Theorem to calculate the distance traveled by each shark, “602 + 452 = c2, c = 75 miles” and “362 + 772 = c2, c = 85 miles”. The student recognized that they needed to “double(d) their distance“ to determine the total distance traveled by the boat. The student also correctly uses the formula for finding “speed = distance`-:` time” to correctly find how fast the boat needs to travel in 5 hours.
Communication
Practitioner
The student correctly identifies the problem, describes the steps to the solution, and states a correct conclusion in the last paragraph. Appropriate formal math language such as Pythagorean Theorem, speed, distance, time, hypotenuse, right triangles, 90`@` turns, formula, doubled, mph are used to share and clarify ideas.
Connections
Practitioner
The student notes the regularity that “they swam that distance in 5 hours (9 am - 2 pm), but they actually had 10 hours (9 am - 7 pm) to swim so I doubled their distance.” The student makes an important observation that sharks “wouldn’t make 90`@` turns, so I found the hypotenuse, a more realistic path.” The student makes a connection with what they understand in the real world about swimming behavior.
Representation
Practitioner
The student uses a diagram to show the distances and directions the sharks traveled. The diagrams are labeled correctly and show that the distance traveled by the shark is likely the hypotenuse between 2 points.
Overall Achievement Level:
Practitioner

Practitioner 3
Scoring Rationale
Problem Solving
Practitioner
The student’s strategy of using a coordinate grid helps them recognize they need “to find the diagonal distance for each shark.” The student uses the Pythagorean Theorem to calculate the diagonal distance of each shark at 2 pm, the formula for speed = `sf ((Distance)/(Time))` to calculate the shark’s speed, and then “you double the sharks speed because the vessel goes the same distance at half the time.” The students answer that “for shark #1 the vessel must go 30 mph whist the vessel would have to go 34 mph to reach shark #2” is correct.
Reasoning & Proof
Practitioner
The student’s arguments are constructed with adequate mathematical basis. The student correctly applies the Pythagorean Theorem to calculate the distance traveled by each shark, “602 + 452 = c2, c = 75 miles” and “362 + 772 = c2, c = 85 miles.” The student correctly justifies the speed of each shark, “75 miles`-:` 5 hours = 15 mph, 85 miles`-:` 5 hours = 17 mph.” The student also shows correct reasoning for how fast the boat would need to travel by doubling the shark’s speed over 5 hours to catch up with the shark in 10 hours.
Communication
Practitioner
A sense of purpose is communicated by the student in the original Question section, “If they wanted to pull up the anchor a 2 pm and end up near one of the sharks, how fast would the vessel have to average?” The student’s approach is provided within the Explanation, “First I had to find the Diagonal distance for each shark” and “I then used the formula for speed = D/T to find each SHARKS speed.” Appropriate formal math language such as average, location, speed, distance, time, “diagonal distance”, “pathgarum therum”, right triangle, formula, double, mph are used to share and clarify ideas.
Connections
Practitioner
The student solves the tasks and notes the pattern “the sharks distance forms a right triangle.” The student explores the relationship “the vessel needs to travel double the speed the sharks go.”
Representation
Practitioner
The student’s use of a coordinate grid and compass rose to illustrate the position of each shark after 5 hours is appropriate and accurate. All necessary labels are provided and the information is correct.
Overall Achievement Level:
Practitioner
Expert
 ,
, 
Expert 1
Scoring Rationale
Problem Solving
Expert
The student’s strategy of drawing a diagram using the provided directional information works to find the distance traveled by the sharks in 5 hours and 10 hours. The student uses their diagram to show that there would be two congruent triangles creating a doubling of the distance traveled. The student’s alternate strategy uses the Pythagorean Theorem to calculate the distance the shark traveled in the first 5 hours and then doubling it to find its distance at 7 pm. The student’s answer of the boat needing to travel 30 mph to catch shark 1 and 34 mph to catch shark 2 is correct. The student recognizes that the shark is likely to travel twice the distance in twice the time to determine how far the shark will have traveled by 7 pm.
Reasoning & Proof
Expert
The student demonstrates correct reasoning by using Pythagorean theorem to find distance traveled on a coordinate grid, a2+ b2 = c2. The student also uses the speed formula to find the correct speed the boat will need to travel to catch both sharks in 5 hours, “Shark 1: `sf text(150)/sf text(5) = sf30`, 30 miles per hour to catch the shark” and “Shark 2: `sf text(170)/sf text(5) = sf34`, 34 miles per hours to catch the shark. The student utilizes their diagram as evidence to support their conclusion of the distance traveled by the shark at 5 hours and 10 hours.
Communication
Expert
The student uses a methodical, organized and sequenced response to communicate their approach. The student correctly identifies the problem, describes the steps to the solution, and states a correct conclusion. Insight is communicated about an efficient strategy when the student states “The sharks will double their distance by 7 pm.” The student utilizes their insight to construct the congruent triangles and to move from “x = 75 miles” to “2x = 150 miles” to find the total distance needed to travel. Appropriate math language, such as diagram, location, difference, double, distance, Pythagorean Theorem, hypotenuse, miles, time, miles per hour, speed is used rigorously to share and clarify ideas.
Connections
Expert
The student uses several alternative strategies for finding the distance traveled and the speed required to make a mathematically relevant math connection. The student explains the phenomena that “the boat has to travel at double the speed of the sharks, because it travels double the distance in the same amount of time.”
Representation
Expert
The student analyzes the relationships between the distance the sharks travel in 5 hours and 10 hours by using congruent triangles to show the total distance traveled. The student uses the diagram to clarify that doubling the time doubles the distance traveled.



MP.1
Make sense of problems and persevere in solving them.