Puzzle Pieces
Andy is putting a puzzle together. The puzzle has one hundred fifty pieces all together.
- The first day Andy puts thirty-six pieces of the puzzle together.
- The second day Andy puts forty-one more pieces of the puzzle together.
- The third day Andy puts sixty-eight more pieces of the puzzle together.
Andy is upset because there are no more puzzle pieces left. How many puzzle pieces does Andy need to finish the puzzle? Show all your mathematical thinking.
Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
- Model
- Diagram/Key
- Number line
- Place value strips
- Number/Hundred chart
- Amount
- Table
- Ordinal numbers: 1st, 2nd, 3rd ...
- Addition/Subtraction
- Difference
- Addend
- Equation
- Total/Sum
- Place value
- Ones, tens, hundreds
- Odd/Even
- More than (>)/Greater than (>)/Less than (<)
- Equivalent/Equal to
- Most/Least
- Per
- Day
A student may independently select a printed number line, number chart, ten frames, graph paper, etc. as they work on a task.
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task for their students, define nouns, promote discussion, access prior knowledge, and inspire engagement and problem solving.
Possible Solutions
Assess
Novice

Novice 1
Scoring Rationale
Problem Solving
Novice
It appears that the student is adding all the numbers located in the task for a total of 285. This strategy does not solve the task. The student's answer, "285 pieces," is not correct.
Reasoning & Proof
Novice
The student does not demonstrate correct reasoning. The student does not understand that the placed puzzle pieces need to be totaled and subtracted from 150 pieces to determine how many pieces are needed to finish the puzzle.
Communication
Novice
The student does not use any mathematical language to communicate their reasoning and proof. Verbs, such as "add," are not included in considering communication as they are considered an action the student takes in their solution.
Connections
Novice
The student does not make a mathematically relevant observation about their solution.
Representation
Novice
The student does not attempt a mathematical representation to solve or portray their solution.
Overall Achievement Level:
Novice
Apprentice
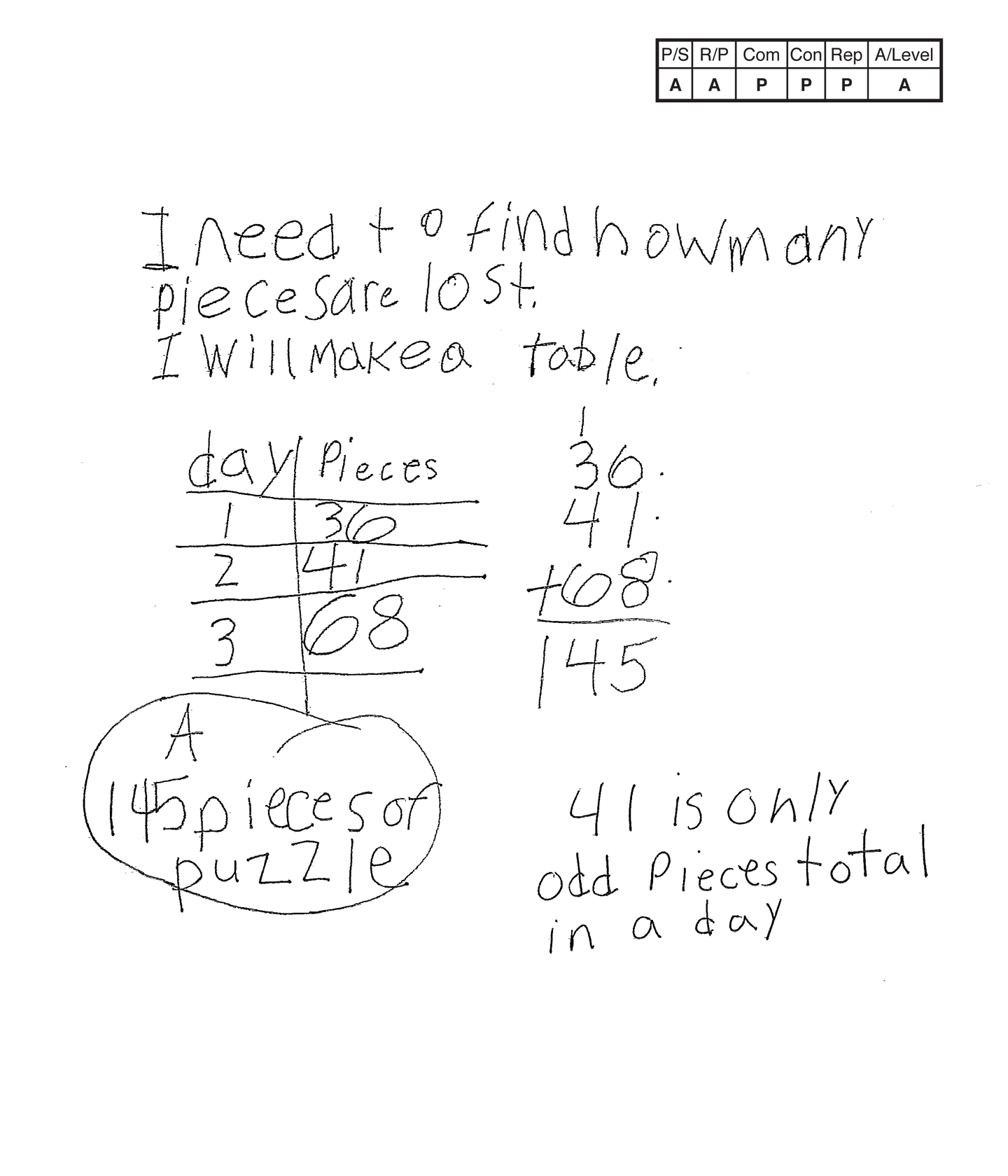
Apprentice 1
Scoring Rationale
Problem Solving
Apprentice
The student has a partially correct strategy. The student totals the puzzle pieces used in the three days. The student does not find the difference between the puzzle pieces used and the original 150 puzzle pieces. The student's answer, "145 pieces of puzzle," is not correct.
Reasoning & Proof
Apprentice
The student uses some correct reasoning of the underlying concepts of the task. The student organizes and determines the 145 puzzle pieces used in three days. The student does not determine how many puzzle pieces are needed to finish the puzzle.
Communication
Practitioner
The student correctly uses the mathematical term day, from the task. The student also correctly uses the mathematical terms table, odd, total.
Connections
Practitioner
The student makes the mathematically relevant observation, "41 is only odd pieces total in a day."
Representation
Practitioner
The student's table is appropriate to the task and accurate. All labels are included and the data is correct.
Overall Achievement Level:
Apprentice
Practitioner
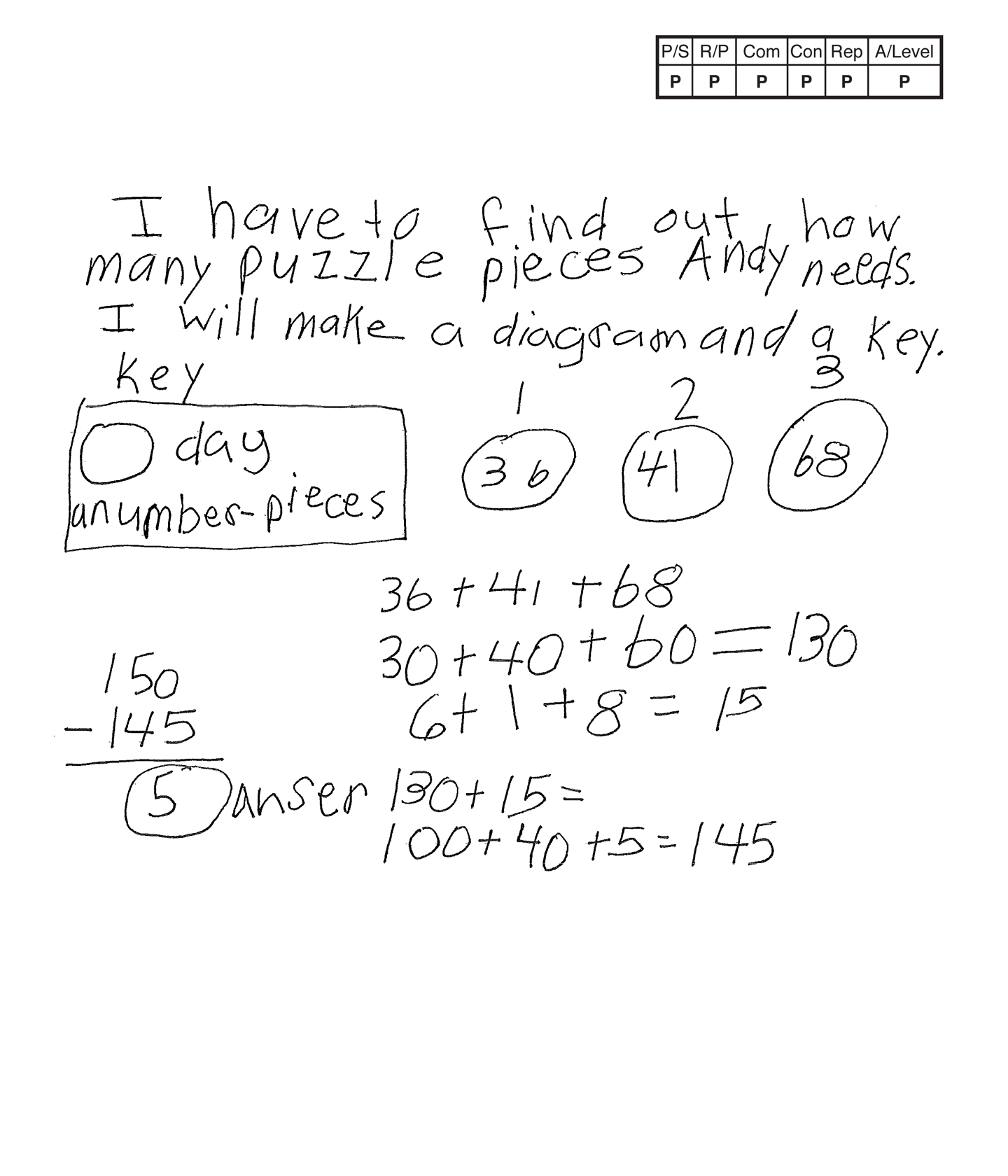 ,
, 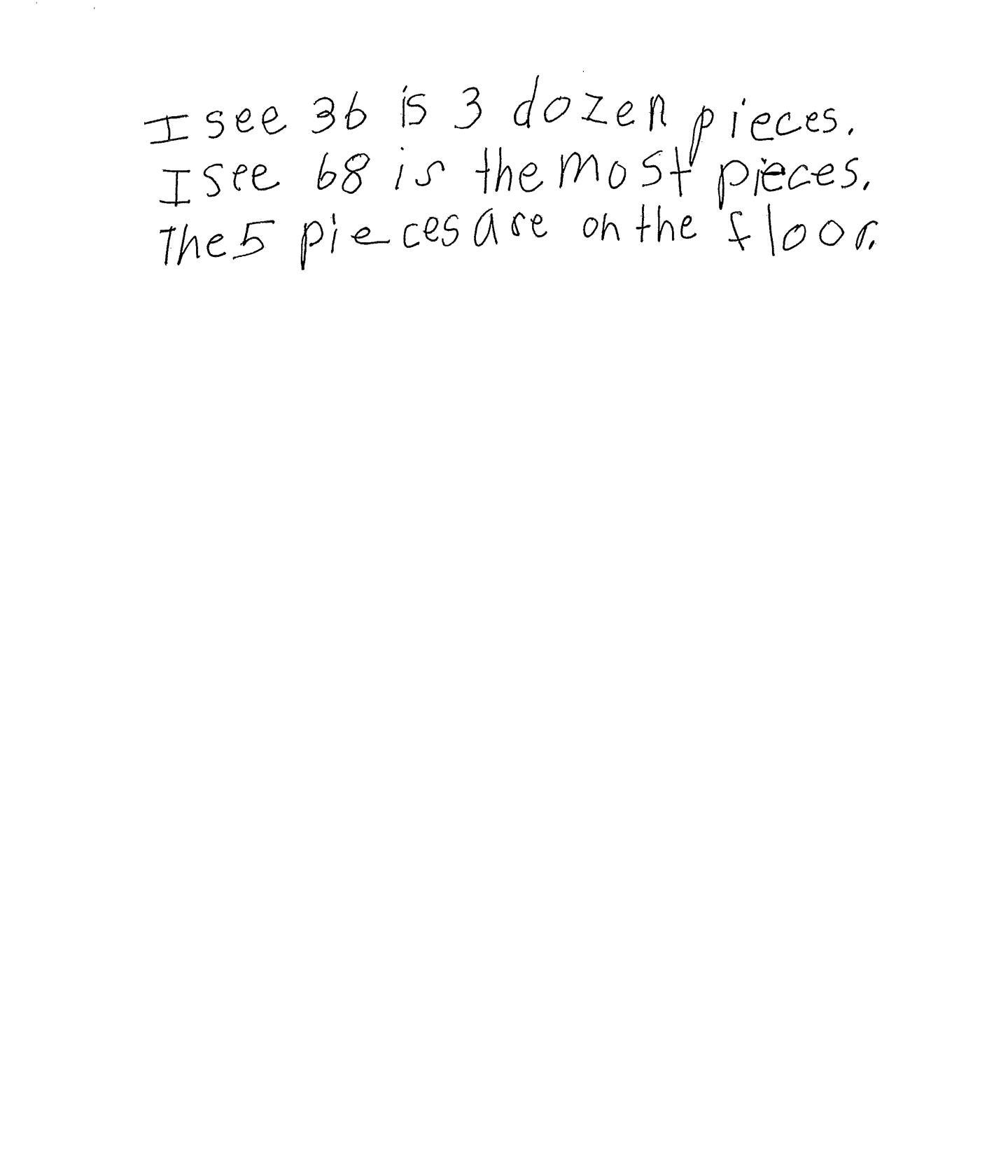
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
The student's strategy of making a diagram of the puzzle pieces used each of three days works to solve part of the task. The student's answer, "5," is correct.
Reasoning & Proof
Practitioner
The student uses correct reasoning of the underlying concepts of the task. The student organizes and determines a total of 145 puzzle pieces are used in three days. The student finds the number of remaining puzzle pieces needed to finish the puzzle by applying subtraction.
Communication
Practitioner
The student correctly uses the mathematical term day from the task. The student also correctly uses the mathematical terms diagram, key, number.
Connections
Practitioner
The student makes the mathematically relevant observations, "I see 36 is 3 dozen pieces" and "I see 68 is the most pieces." The student's statement, "The 5 pieces are on the floor," is not considered a mathematically relevant statement. This comment could lead to an engaging classroom writing activity determining where those five missing pieces are.
Representation
Practitioner
The student's diagram is appropriate to the task and accurate. A key defines the days and puzzle pieces. The entered "numbers" are correct.
Overall Achievement Level:
Practitioner
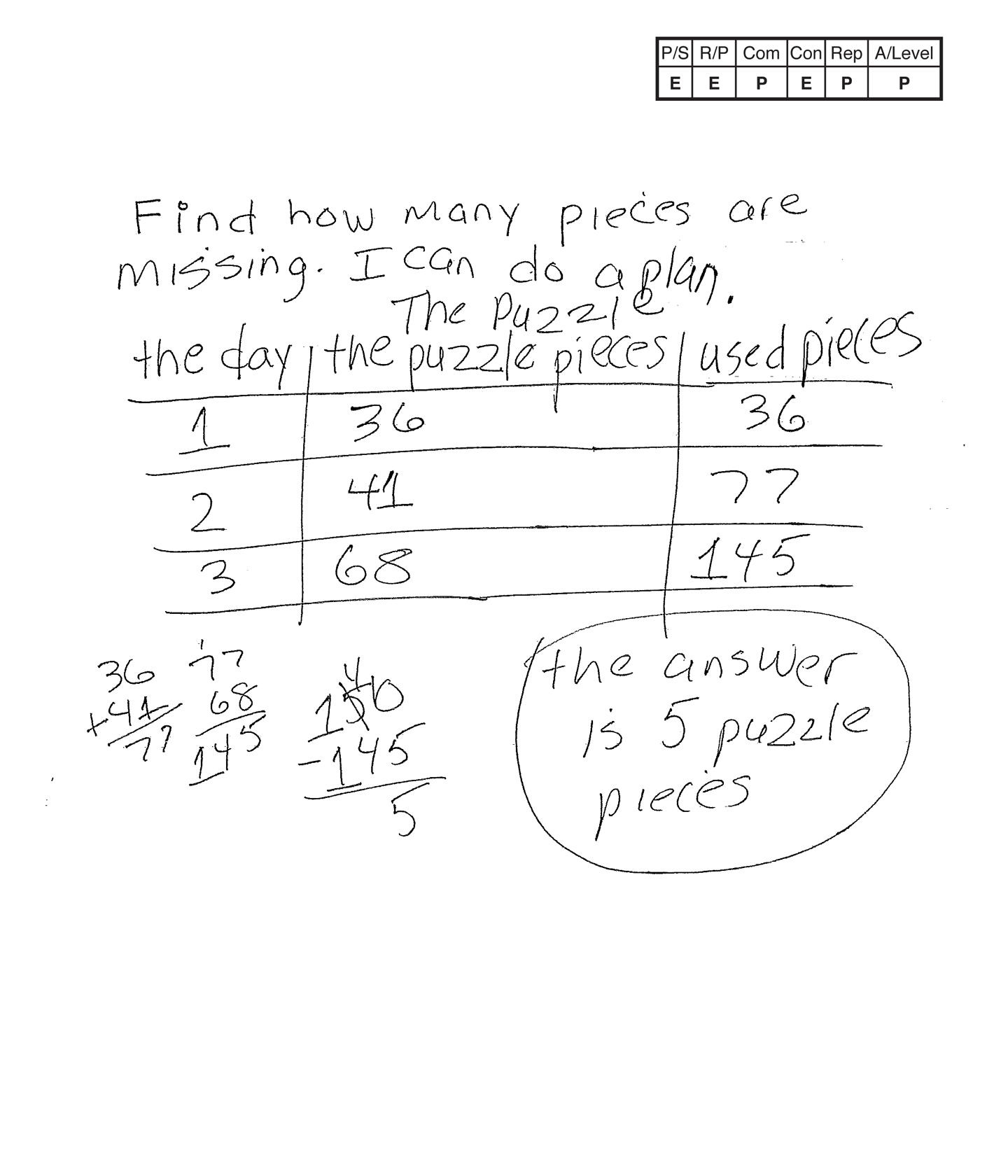 ,
, 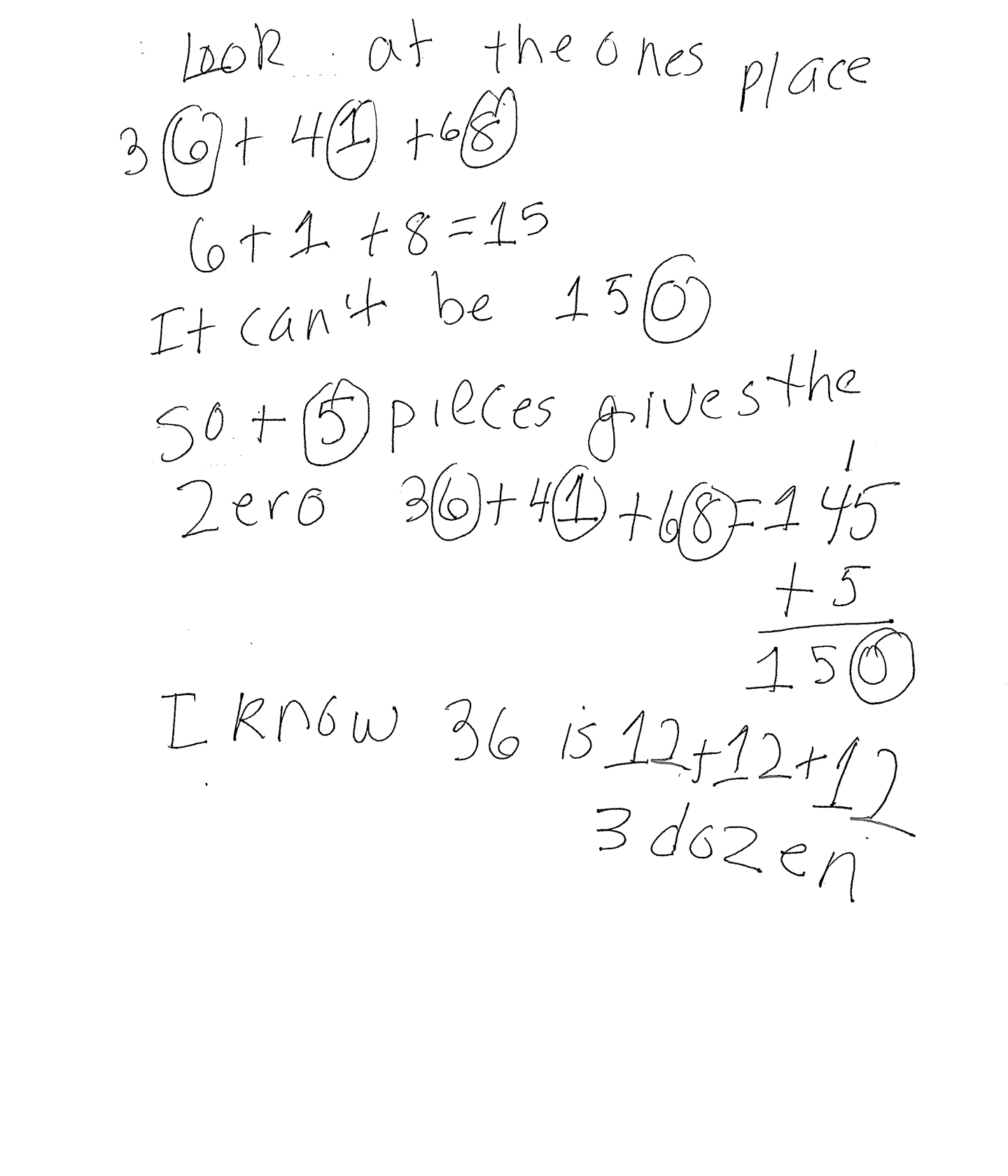
Practitioner 2
Scoring Rationale
Problem Solving
Expert
The student's strategy of making a table of the day, puzzle pieces and total puzzle pieces works to solve part of the task and arrives at an answer by applying subtraction. The student's answer, "the answer is 5 puzzle pieces," is correct. The student shows evidence of analyzing the situation in mathematical terms. The student explores the numbers in the ones place and determines that a total of 150 pieces is not possible.
Reasoning & Proof
Expert
The student demonstrates correct reasoning of the underlying concepts of the problem. The student organizes and determines a total of 145 puzzle pieces are used in three days. The student finds the number of remaining puzzle pieces needed to finish the puzzle by applying subtraction. The student explains the phenomenon of how some sets of numbers can not have a total with a zero in the ones place. The student uses that thinking to explain how they realized that five puzzle pieces must be missing.
Communication
Practitioner
The student correctly uses the mathematical term day, from the problem. The student also correctly uses the mathematical terms ones place, dozen.
Connections
Expert
The student makes the Practitioner connection, "I know 36 is 12 + 12 + 12, 3 dozen." The student makes an Expert connection by extending their understanding of this task to place value. "Look at the ones place 36 + 41 + 68, 6 + 1 + 8 = 15. It can't be 150. So + 5 pieces gives the zero. 36 + 41 + 68 = 145, 145 + 5 = 150."
Representation
Practitioner
The student's table is appropriate to the task and accurate. All labels are included and the data is correct.
Overall Achievement Level:
Practitioner
Expert
 ,
, 
Expert 1
Scoring Rationale
Problem Solving
Expert
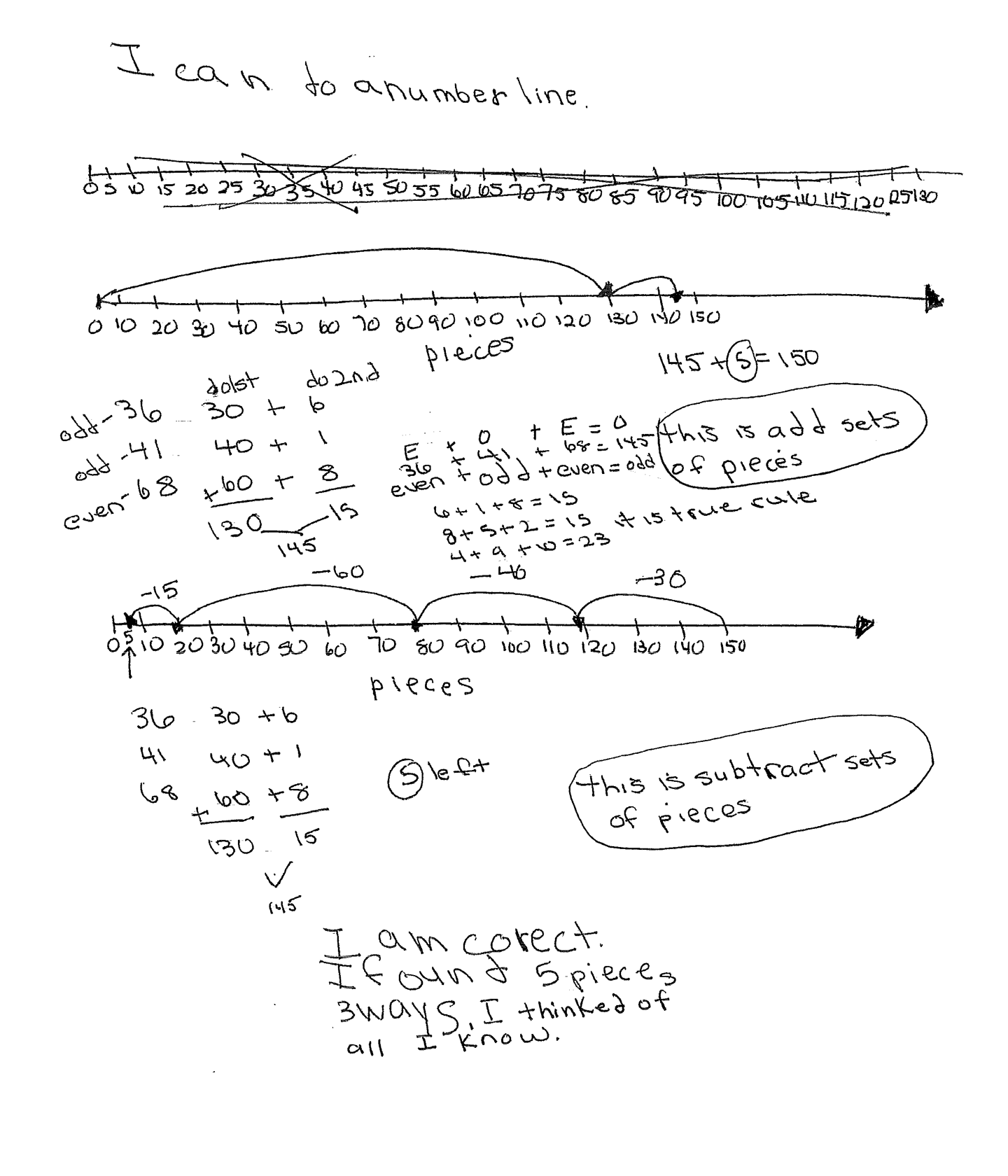
The student's strategy of making a table of the days, puzzle pieces and total puzzle pieces works to solve part of the task. The student applies subtraction and states a correct answer, "5 pieces." The student shows evidence of analyzing the situation in mathematical terms. The student explores the numbers in the ones place and determines that a total of 150 pieces is not possible. The student also applies the Even + Odd + Even = Odd rule to support their analysis. The student also verifies that their solution is correct by using number lines as a new strategy.
Reasoning & Proof
Expert
The student uses correct reasoning of the underlying concepts of the task. The student organizes and determines a total of 145 puzzle pieces are used in three days. The student finds the number of remaining puzzle pieces needed to finish the puzzle by applying subtraction. The student explains the phenomenon that when adding, some sets of numbers can not have a total with a zero in the ones place. The student uses this thinking to explain how they realized that some puzzle pieces must be missing. The student uses number lines to verify that the data in their table is correct.
Communication
Expert
The student correctly uses the mathematical term day from the task. The student also correctly uses the mathematical terms table, 1st, 2nd, 3rd, total, dozen, most, sum, number line, odd, even, sets, rule. The student correctly uses the symbolic notation E + O + E = O and defines E and O under the numbers.
Connections
Expert
The student makes the mathematically relevant Practitioner observation, "36 is 3 dozen pieces" and "He puts the most pieces in on the 3rd day." The student makes the Expert connection, "36 41 68, 6 + 1 + 8 = 15. The sum does not end in 0 so they can not add up to 150." The student also states E + O + E = O, 36 + 41 + 68 = 145, even + odd + even = odd." The student applies this rule by using the equations, 6 + 1 + 8 = 15, 8 + 5 + 2 = 15, 4 + 9 + 10 + 23, and states, "it is a true rule." The student also verifies their answer by using two number lines to arrive at 150 pieces. The first number line considers addition and the second number line considers subtraction. The student states, "I am correct. I found 5 pieces 3 ways. I thinked of all I know."
Representation
Expert
The student's table is appropriate to the task and accurate. All labels are included and the data is correct. The student attempts a number line and discards it as they realized the paper is too short to have a number line using increments of five. The student makes two correct number lines with increments of ten. The student indicates that the numbers represent pieces. The student compares these two number lines with their table to verify that their answer is correct.



MP.1
Make sense of problems and persevere in solving them.