Herding Cats
Maru owns a free-roam cat rescue. Maru is working to enclose her roaming area with a cat-safe electric fence. Maru knows the cost of an electric fence installed is $0.89 per foot. The Meow Safe Fencing Company has provided an estimated price of $3,190 for fencing in the total property.
The boundaries for the property can be described using coordinates on a scaled grid overlaid on an aerial photo. Each unit is 30 feet. The boundary coordinates are (1, 0), (25, 0), (25, 22), (21, 22), (21, 16), (5, 16), (5, 22), and (1, 22).
Write a letter to the Meow Safe Fencing Company either accepting or rejecting their offer. Be sure to include all of your mathematical thinking.

Plan
Underlying Mathematical Concepts
Possible Problem-Solving Strategies
Formal Mathematical Language and Symbolic Notation
Teacher Notes:
Possible misconceptions that students may encounter:
- Determine perimeter and cost based on number of units without scaling by 30.
- Interpreting and plot coordinates as (y, x) instead of (x, y).
Suggested Materials
Engagement Image:
Teachers may project the image below to launch this task in the classroom, to prepare students, to promote discussion, and to inspire engagement and problem solving.
Possible Solutions
Assess
Novice

Novice 1
Scoring Rationale
Problem Solving
Novice
The student confuses needing to find the perimeter of the enclosed space with their strategy of finding the area of the total yard. The student appears to divide the figure into rectangles and find the areas of these figures. This strategy will never lead to a correct solution for this question.
Reasoning & Proof
Novice
The student shows little correct reasoning in attempting to solve the task. No correct reasoning is present in finding the perimeter of the yard. Numerous calculations are present, but no reasoning is provided for what is being calculated.
Communication
Apprentice
The written explanation given for the work is limited and unclear. Work is difficult to understand and hard to follow. Significant interpretation is required to understand the student's strategy by the reader. The use of math language is limited.
Connections
Novice
No connections are present or attempted by the student.
Representation
Apprentice
Based on the drawing included, the student appears to correctly plot the coordinates given on a coordinate plane to create a diagram of the fenced area. The diagram is not labeled. The student then attempts to break the yard into rectangles to find the area of the total yard. The student does utilize area models for several calculations, although we are unsure what they are working to find.
Overall Achievement Level:
Novice
Apprentice
 ,
, 
Apprentice 1
Scoring Rationale
Problem Solving
Apprentice
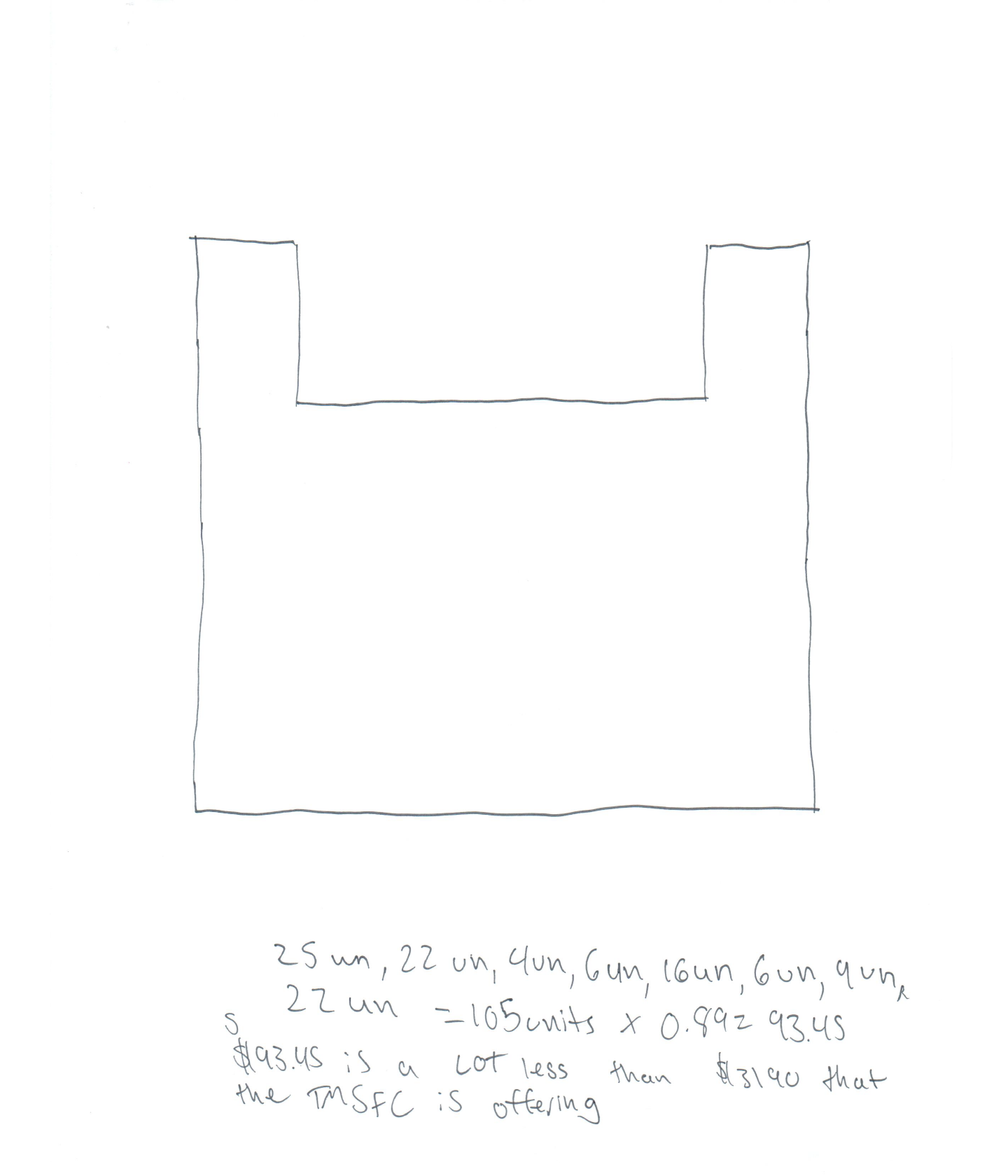
The student correctly plots and connects the coordinates given to form a diagram of the fenced area. The student incorrectly calculates the perimeter of the polygon in unit lengths (records the bottom segment as 25 units instead of 24 units) to be 105 units instead of 104 units. The student also incorrectly uses 105 units as the perimeter, failing to multiply the measure by 30 feet/unit to get the perimeter in feet. The student multiplies the incorrect perimeter by $.89 (cost/foot) to get the incorrect cost of $93.45. These incorrect calculations still lead the student to the correct decision to reject the offer from the fence company.
Reasoning & Proof
Apprentice
The student demonstrates some understanding of the underlying concepts of the task, but fails to use the unit rate of 30 feet/unit length to find the perimeter in feet, which is needed to determine cost using the unit rate $.89 cost/foot. The student is inconsistent in finding the unit lengths of all sides of the figure. Errors in computation of the perimeter in unit lengths lead to subsequent errors in the solution process. The calculation 25un, 22un, 4un, 6un, 16un, 6un, 4un, 22un = 105 units x 0.89 = 93.45 is also an incorrect mathematical statement.
Communication
Practitioner
The student presents a sequenced response to communicate work. The explanations of the steps to the solution process are clear and easy to follow even though some of the calculations are incorrect. Math vocabulary is limited, yet appropriate.
Connections
Apprentice
The student attempts to make a connection but it lacks contextual relevance.
Representation
Apprentice
The student draws a diagram of the fenced area, but some of the unit lengths given for the sides are missing or incorrect. The diagrams units are not labeled.
Overall Achievement Level:
Apprentice
 ,
, 
Apprentice 2
Scoring Rationale
Problem Solving
Apprentice
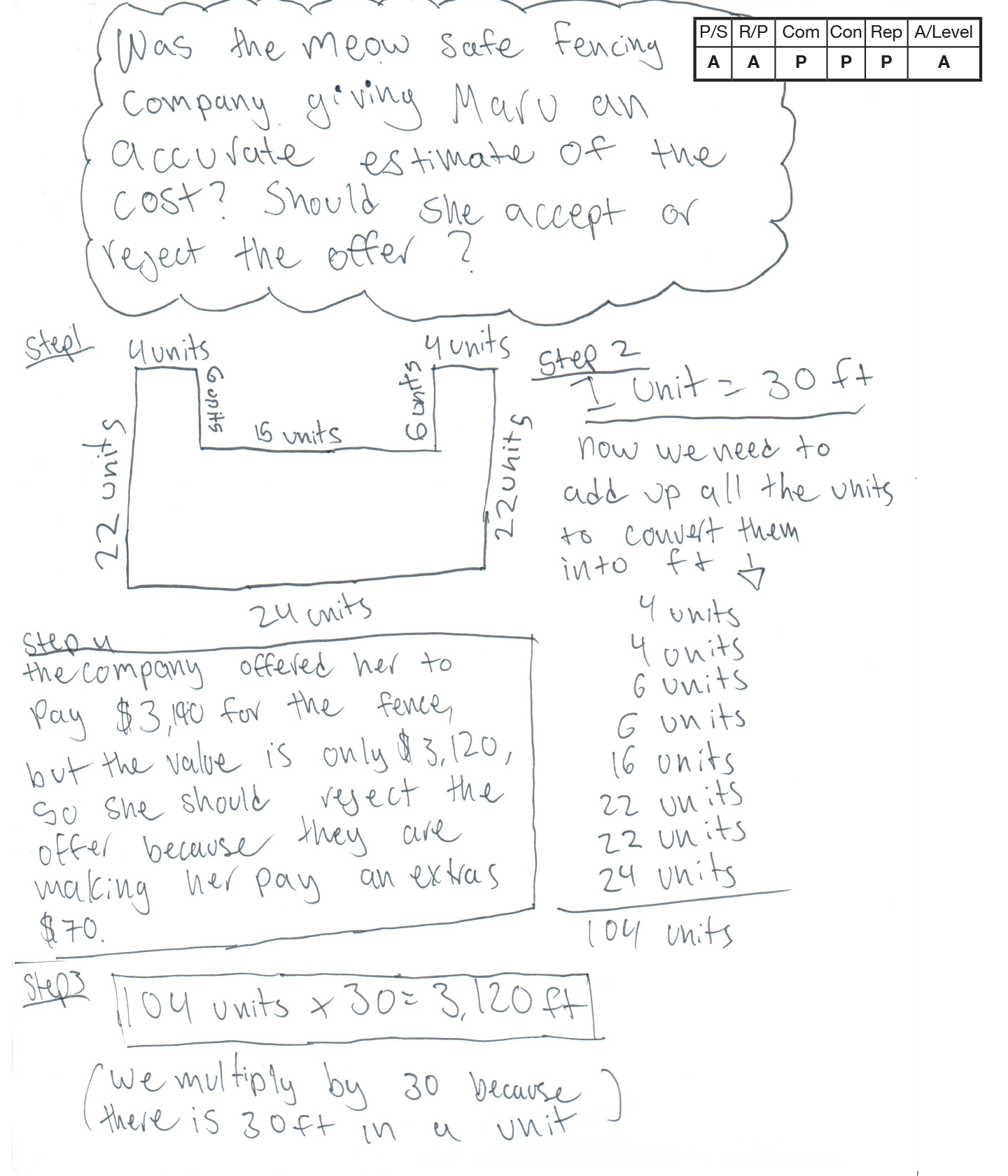
The student’s strategy of creating a representation and finding the number of units, leading to the number of feet in the perimeter, is correct. However, the student fails to multiply the number of total feet by $0.89 to successfully solve the task. Despite failing to make the calculation of converting from total perimeter to a cost, the student does arrive at a correct answer.
Reasoning & Proof
Apprentice
The student provides some correct reasoning for several of the steps. However, the argument is incomplete and inaccurate because the student fails to multiply the total perimeter by the $0.89 per foot, leading to an incorrect cost for the fencing.
Communication
Practitioner
The student demonstrates a sense of purpose, clearly communicating this in the task statement at the beginning of the solution. The student’s overall approach is clear, organized and sequenced. Formal mathematical language, labels and symbolic notation are evident.
Connections
Practitioner
The student extends the task by finding the difference between the Meow Safe’s offer and their calculations.
Representation
Practitioner
There is an accurate and appropriate mathematical representation created in step 1 of the task. This representation is constructed to help portray their calculations and strategy for arriving at their final answer.
Overall Achievement Level:
Apprentice
Practitioner
 ,
, 
Practitioner 1
Scoring Rationale
Problem Solving
Practitioner
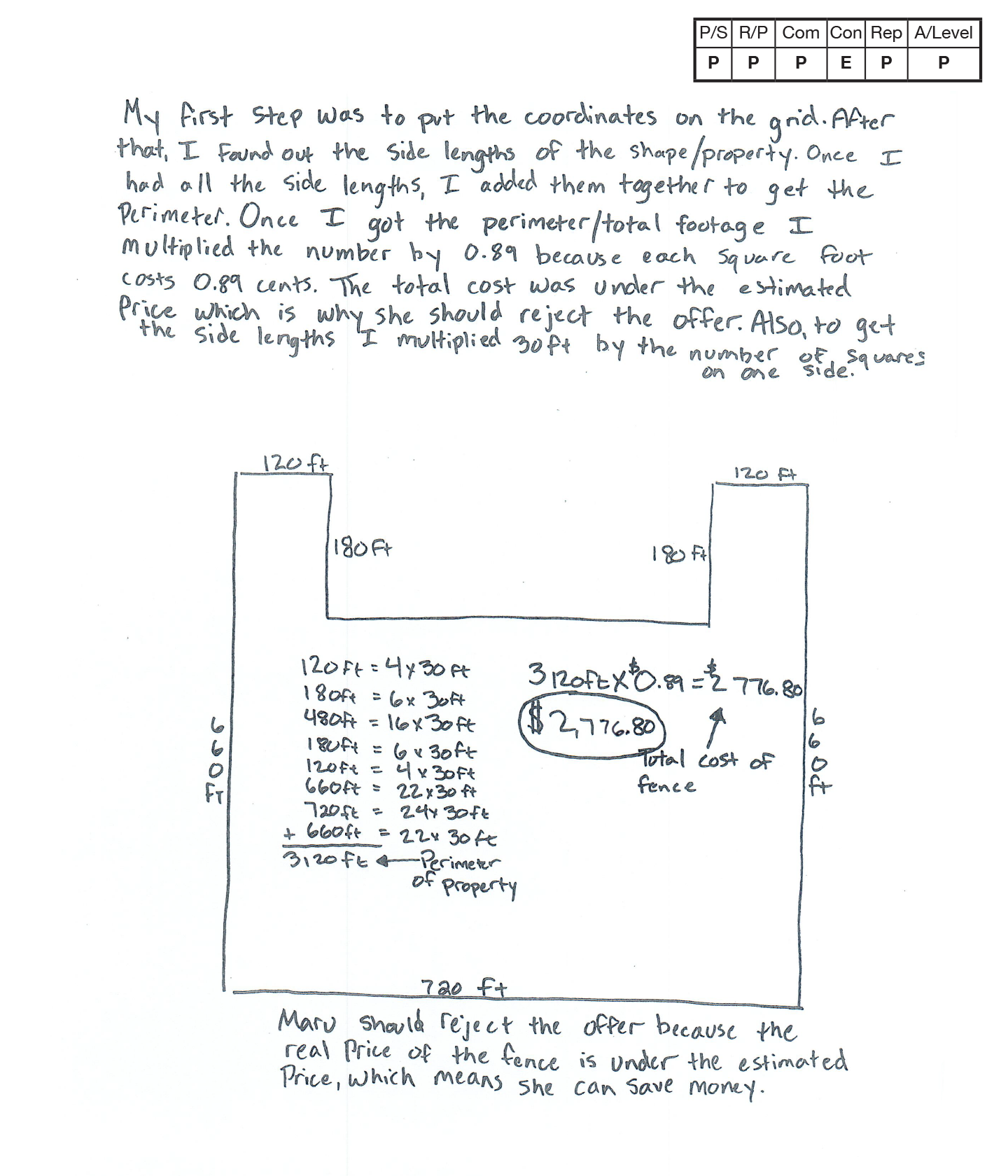
The student correctly plots the points given to create a diagram of the fenced area. The student determines the unit lengths of each line segment and converts these to feet by multiplying each value by 30 (feet per unit length). The student correctly determines the cost at $2776.80 by multiplying 3120 feet by $.89 (cost/foot). The student correctly determines that the offer from the fence company should be rejected.
Reasoning & Proof
Practitioner
The student’s argument is sequenced, logical and easy to follow. The student demonstrates correct reasoning of the underlying concepts of the task. The student determines the length in feet of the fence and then calculates the total cost by multiplying by the unit rate of $.89. Calculations are correct and support the solution given.
Communication
Practitioner
The student uses an organized and sequenced response to communicate work. The student explains each step to the solution process. Work is clear and easy to follow. Appropriate math language is used.
Connections
Expert
The student describes a second way the task can be solved (but does not actually show the calculations). The student also makes a connection between the mathematics in the task and how the strategy for solving the task could be extended to other cases, “when your coding."
Representation
Practitioner
The student plots the given points to create a diagram of the fenced area on a coordinate grid. The student correctly labels the length of each line segment in feet on the diagram.
Overall Achievement Level:
Practitioner
 ,
,  ,
, 
Practitioner 2
Scoring Rationale
Problem Solving
Practitioner
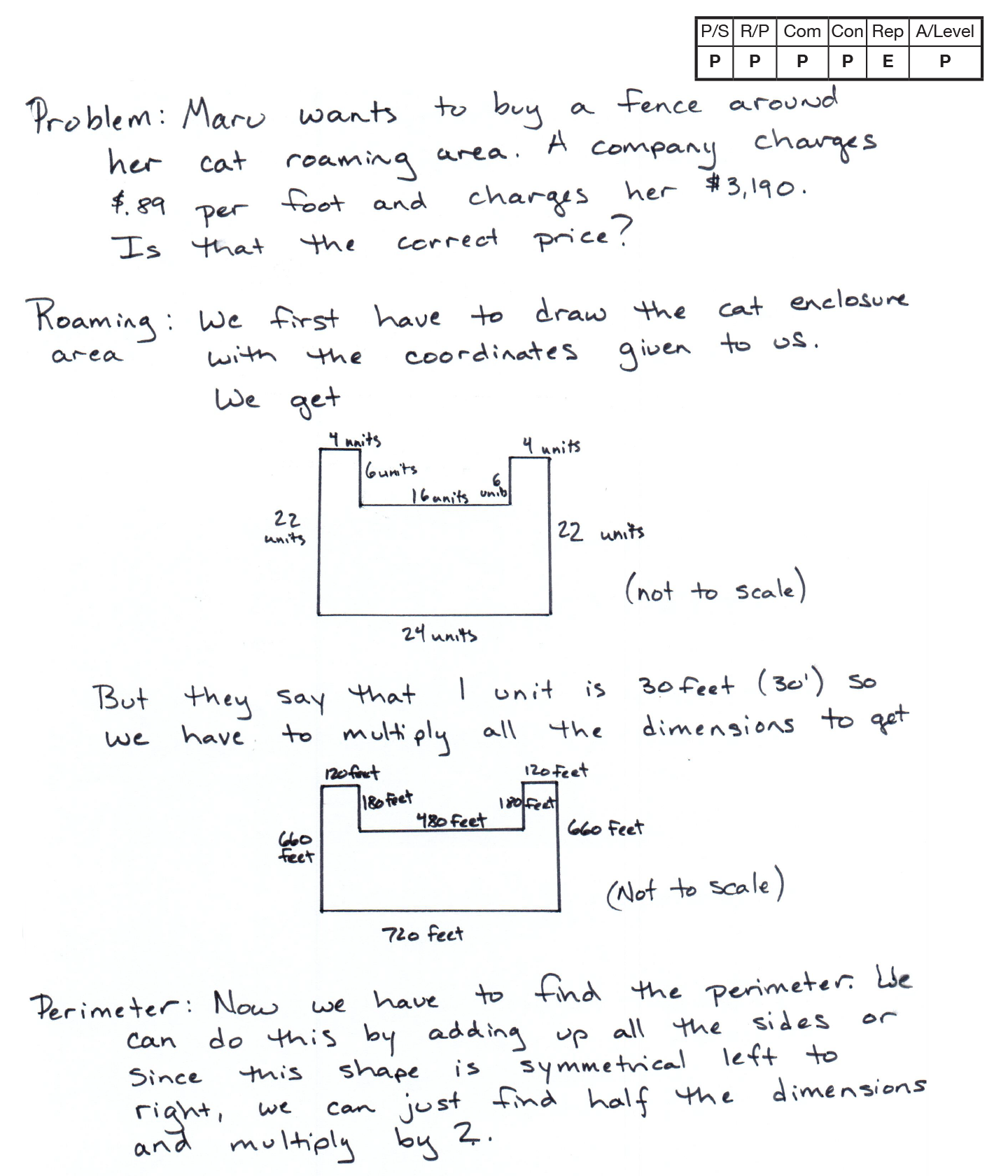
The student correctly plots the points given to create a diagram of the fenced area. The student determines the unit lengths of each line segment and converts these to feet by multiplying each value by 30 (feet per unit length). The student correctly determines the cost at $2,776.80 by multiplying 3,120 feet by $.89 (cost/foot). The student correctly determines that the offer from the fence company should be rejected.
Reasoning & Proof
Practitioner
The student correctly plots points on a coordinate grid, finds the perimeter of the polygon created in unit lengths, and then converts units into feet in the diagram. Calculations for the total cost are present and correct. The student demonstrates an interesting strategy of finding half the total perimeter to enclose and then multiplying by 2 to find the other half of the perimeter.
Communication
Practitioner
The student uses an organized, sequenced, and labeled response to communicate work. The student identifies the task to be solved, explains each step in the solution process, and explicitly states the solution. Units of measure are accurately recorded. The student uses appropriate math language.
Connections
Practitioner
The student explores a mathematical phenomenon within their solution, “since this shape is symmetrical left to right, we can just find half the dimensions and multiply by 2.” This secondary strategy recognizes an interesting pattern in finding perimeter of symmetrical shapes.
Representation
Expert
The student creates two correct diagrams of the fenced area to help analyze the relationships between the different measurement for the perimeter of units versus feet.
Overall Achievement Level:
Practitioner
Expert
 ,
, 
Expert 1
Scoring Rationale
Problem Solving
Expert
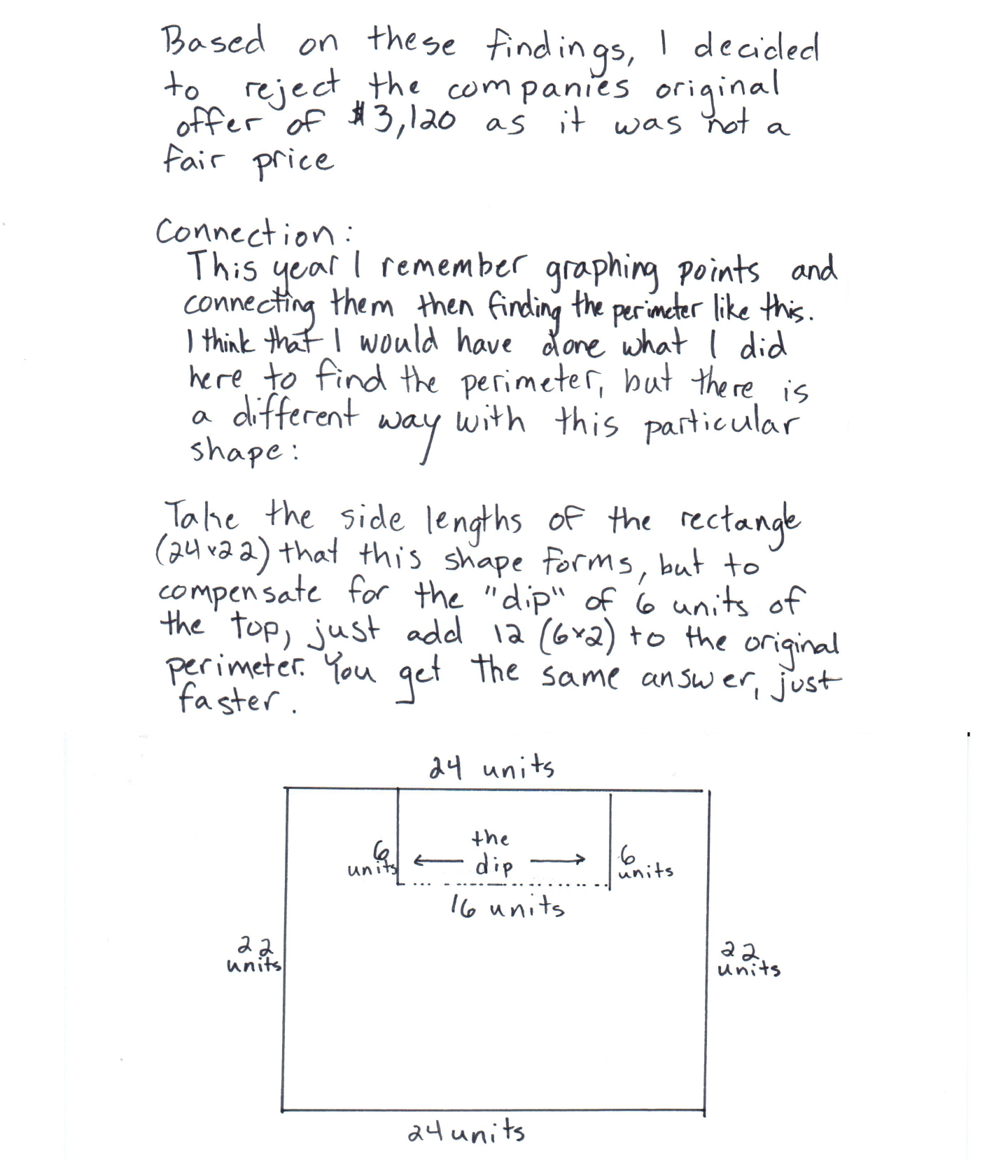
The student provides an effective strategy and a second more efficient strategy to solve the task. The alternative strategy at the end is considered, which shows evidence of the student analyzing the situation and defining a more efficient strategy to solve the task, “but there is a different way…” The student then describes and diagrams this alternative strategy.
Reasoning & Proof
Expert
The student provides a systematic mathematical justification throughout. Because the student also supports their idea mathematically for an alternative strategy on how to solve the task more efficiently, “compensate for the 'dip' of 6 units at the top…” this student achieves Expert level work. Calculations are correct that support the solution.
Communication
Expert
The student uses an organized, sequenced, and labeled response to communicate their work. The student provides insight into the efficiency of their original strategy and defines a more efficient method for reaching the same perimeter. Formal math language is used throughout to communicate their ideas.
Connections
Expert
The student provides a deeper understanding of the mathematics in the task as they describe their alternative strategy to solve the task faster, “compensate for the 'dip' of 6 units at the top…” Experts articulate connections between various strategies for solving the task.
Representation
Expert
The student constructs a representation that clarifies their idea of using the perimeter of the rectangle “that this shape forms” plus the “the dip.” The construction of the two representations helps to clarify how they can each be used to solve the overall question.



MP.2
Reason abstractly and quantitatively.